Урок 14
§9. Восьмеричная система счисления

Содержание урока

Восьмеричная система счисления

Связь с двоичной системой счисления

Алгоритм перевода восьмеричного числа в двоичную систему счисления

Алгоритм перевода двоичного числа в восьмеричную систему счисления

Арифметические действия

Применение восьмеричной системы

Выводы. Интеллект-карта

Вопросы и задания

Восьмеричная система счисления

Восьмеричная система счисления (система с основанием 8) использует 8 цифр: от 0 до 7.

Как бы вы записали числа 8, 9, 18, 19, 89, 98, если бы цифр 8 и 9 не существовало?

Какие числа записаны в восьмеричной системе неверно: 345₈, 576₈, 961₈, 1823₈? Как вы рассуждали?

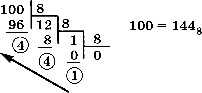
Переведите в восьмеричную систему счисления числа 16, 25, 55, 75, 98, 127.

Запись некоторого числа в восьмеричной системе счисления заканчивается на 0. Что можно сказать о свойствах этого числа?

Запись некоторого числа в восьмеричной системе счисления заканчивается на 3. Что можно сказать о свойствах этого числа?

Платон перевёл некоторое число из десятичной системы в восьмеричную, полученная запись содержит 2 цифры. Какое это могло быть число (назовите наименьшее и наибольшее возможные значения)?

Для перевода числа из восьмеричной системы в десятичную значение каждой цифры умножают на 8 в степени, равной разряду этой цифры, и полученные произведения складывают:

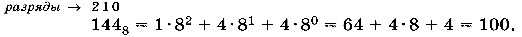
Фактически число записывается в развёрнутой форме.

Переведите числа 16₈, 35₈, 57₈, 103₈, 177₈, 234₈ в десятичную систему счисления.

Следующая страница Связь с двоичной системой счисления

Cкачать материалы урока