Уроки 6 - 7
§ 1.2. Представление чисел в компьютере

1.2.1. Представление целых чисел

Оперативная память компьютера состоит из ячеек, каждая из которых представляет собой физическую систему, состоящую из некоторого числа однородных элементов. Эти элементы обладают двумя устойчивыми состояниями, одно из которых соответствует нулю, а другое — единице. Каждый такой элемент служит для хранения одного из битов — разряда двоичного числа. Именно поэтому каждый элемент ячейки называют битом или разрядом (рис. 1.2).

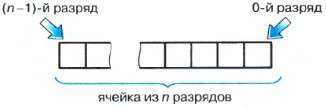
Рис. 1.2. Ячейка памяти

Для компьютерного представления целых чисел используется несколько различных способов, отличающихся друг от друга количеством разрядов (под целые числа обычно отводится 8, 16, 32 или 64 разряда) и наличием или отсутствием знакового разряда. Беззнаковое представление можно использовать только для неотрицательных целых чисел, отрицательные числа представляются только в знаковом виде.

Беззнаковое представление используется для таких объектов, как адреса ячеек, всевозможные счётчики (например, число символов в тексте), а также числа, обозначающие дату и время, размеры графических изображений в пикселях и т. д.

Максимальное значение целого неотрицательного числа достигается в случае, когда во всех разрядах ячейки хранятся единицы. Для n-разрядного представления оно будет равно 2ⁿ-1. Минимальное число соответствует п нулям, хранящимся в n разрядах памяти, и равно нулю.

Ниже приведены максимальные значения для беззнаковых целых n-разрядных чисел:

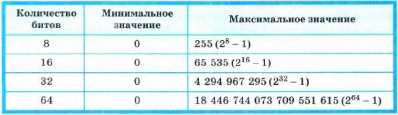
Для получения компьютерного представления беззнакового целого числа достаточно перевести число в двоичную систему счисления и дополнить полученный результат слева нулями до стандартной разрядности.

Пример 1. Число 53₁₀ = 110101₂ в восьмиразрядном представлении имеет вид:

Это же число 53 в шестнадцати разрядах будет записано следующим образом:

При представлении со знаком самый старший (левый) разряд отводится под знак числа, остальные разряды — под само число. Если число положительное, то в знаковый разряд помещается 0, если число отрицательное — 1. Такое представление чисел называется прямым кодом.

В компьютере прямые коды используются для хранения положительных чисел в запоминающих устройствах, для выполнения операций с положительными числами.

На сайте Федерального центра информационно-образовательных ресурсов (http://fcior.edu.ru/) размещён информационный модуль «Число и его компьютерный код». С помощью этого ресурса вы можете получить дополнительную информацию по изучаемой теме.

Для выполнения операций с отрицательными числами используется дополнительный код, позволяющий заменить операцию вычитания сложением. Узнать алгоритм образования дополнительного кода вы можете с помощью информационного модуля «Дополнительный код», размещённого на сайте Федерального центра информационно-образовательных ресурсов (http://fcior.edu.ru/).

1.2.2. Представление вещественных чисел

Любое вещественное число А может быть записано в экспоненциальной форме:

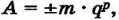где:

m — мантисса числа;
q — основание системы счисления;
p — порядок числа.

Например, число 472 000 000 может быть представлено так: 4,72 • 10⁸, 47,2 • 10⁷, 472,0 • 10⁶ и т. д.

С экспоненциальной формой записи чисел вы могли встречаться при выполнении вычислений с помощью калькулятора, когда в качестве ответа получали записи следующего вида: 4.72Е+8.

Здесь знак «Е» обозначает основание десятичной системы счисления и читается как «умножить на десять в степени».

Из приведённого выше примера видно, что положение запятой в записи числа может изменяться.

Для единообразия мантиссу обычно записывают как правильную дробь, имеющую после запятой цифру, отличную от нуля. В этом случае число 472 000 000 будет представлено как 0,472 • 10⁹.

Вещественное число может занимать в памяти компьютера 32 или 64 разряда. При этом выделяются разряды для хранения знака мантиссы, знака порядка, порядка и мантиссы.

Пример:

Диапазон представления вещественных чисел определяется количеством разрядов, отведённых для хранения порядка числа, а точность определяется количеством разрядов, отведённых для хранения мантиссы.

Максимальное значение порядка числа для приведённого выше примера составляет 1111111₂ = 127₁₀, и, следовательно, максимальное значение числа:

0,11111111111111111111111 • 10^1111111

Попытайтесь самостоятельно выяснить, каков десятичный эквивалент этой величины.

Широкий диапазон представления вещественных чисел важен для решения научных и инженерных задач. Вместе с тем следует понимать, что алгоритмы обработки таких чисел более трудоёмки по сравнению с алгоритмами обработки целых чисел.

САМОЕ ГЛАВНОЕ

Для компьютерного представления целых чисел используются несколько различных способов, отличающихся друг от друга количеством разрядов (8, 16, 32 или 64) и наличием или отсутствием знакового разряда.

Для представления беззнакового целого числа его следует перевести в двоичную систему счисления и дополнить полученный результат слева нулями до стандартной разрядности.

При представлении со знаком самый старший разряд отводится под знак числа, остальные разряды — под само число. Бели число положительное, то в знаковый разряд помещается 0, если число отрицательное, то 1. Положительные числа хранятся в компьютере в прямом коде, отрицательные — в дополнительном.

При хранении в компьютере вещественных чисел выделяются разряды на хранение знака порядка числа, самого порядка, знака мантиссы и мантиссы. При этом любое число записывается так:

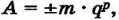где:

m — мантисса числа;
q — основание системы счисления;
p — порядок числа.

Вопросы и задания

1. Ознакомьтесь с материалами презентации к параграфу, содержащейся в электронном приложении к учебнику. Используйте эти материалы при подготовке ответов на вопросы и выполнении заданий.

2. Как в памяти компьютера представляются целые положительные и отрицательные числа?

3. Любое целое число можно рассматривать как вещественное, но с нулевой дробной частью. Обоснуйте целесообразность наличия особых способов компьютерного представления целых чисел.

4. Представьте число 63₁₀ в беззнаковом 8-разрядном формате.

5. Найдите десятичные эквиваленты чисел по их прямым кодам, записанным в 8-разрядном формате со знаком:

а) 01001100;
б) 00010101.

6. Какие из чисел 443₈, 101010₂, 256₁₀ можно сохранить в 8-разрядном формате?

7. Запишите следующие числа в естественной форме:

а) 0,3800456 • 10²;
б) 0,245 • 10^-3;
в) 1,256900Е+5;
г) 9,569120Е-3.

8. Запишите число 2010,0102₁₀ пятью различными способами в экспоненциальной форме.

9. Запишите следующие числа в экспоненциальной форме с нормализованной мантиссой — правильной дробью, имеющей после запятой цифру, отличную от нуля:

а) 217,934₁₀;
б) 75321₁₀;
в) 0,00101₁₀.

10. Изобразите схему, связывающую основные понятия, рассмотренные в данном параграфе.

Электронное приложение к уроку

Cкачать материалы урока