Урок 14
§ 2.1. Алгоритмы и исполнители

2.1.1. Понятие алгоритма

Каждый человек в повседневной жизни, в учёбе или на работе решает огромное количество задач самой разной сложности. Сложные задачи требуют длительных размышлений для нахождения решения; простые и привычные задачи человек решает не задумываясь, автоматически. В большинстве случаев решение каждой задачи можно разбить на простые этапы (шаги). Для многих таких задач (установка программного обеспечения, сборка шкафа, создание сайта, эксплуатация технического устройства, покупка авиабилета через Интернет и т. д.) уже разработаны и предлагаются пошаговые инструкции, при последовательном выполнении которых можно прийти к желаемому результату.

Пример 1. Задача «Найти среднее арифметическое двух чисел» решается в три шага:

1) задумать два числа;
2) сложить два задуманных числа;
3) полученную сумму разделить на 2.

Пример 2. Задача «Внести деньги на счёт телефона» подразделяется на следующие шаги:

1) подойти к терминалу по оплате платежей;
2) выбрать оператора связи;
3) ввести номер телефона;
4) проверить правильность введённого номера;
5) вставить денежную купюру в купюроприёмник;
6) дождаться сообщения о зачислении денег на счёт;
7) получить чек.

Пример 3. Этапы решения задачи «Нарисовать весёлого ёжика» представлены графически:

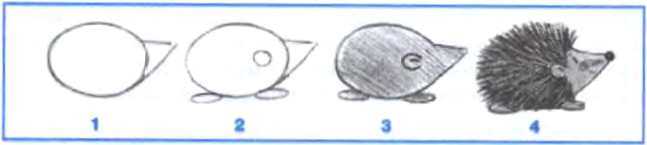
Нахождение среднего арифметического, внесение денег на телефонный счёт и рисование ежа — на первый взгляд совершенно разные процессы. Но у них есть общая черта: каждый из этих процессов описывается последовательностями кратких указаний, точное следование которым позволяет получить требуемый результат. Последовательности указаний, приведённые в примерах 1-3, являются алгоритмами решения соответствующих задач. Исполнитель этих алгоритмов — человек.

Алгоритм может представлять собой описание некоторой последовательности вычислений (пример 1) или шагов нематематического характера (примеры 2-3). Но в любом случае перед его разработкой должны быть чётко определены начальные условия (исходные данные) и то, что предстоит получить (результат). Можно сказать, что алгоритм — это описание последовательности шагов в решении задачи, приводящих от исходных данных к требуемому результату.

В общем виде схему работы алгоритма можно представить следующим образом (рис. 2.1).

Рис. 2.1. Общая схема работы алгоритма

Алгоритмами являются изучаемые в школе правила сложения, вычитания, умножения и деления чисел, многие грамматические правила, правила геометрических построений и т. д.

Анимации «Работа с алгоритмом» (193576), «Наибольший общий делитель» (170363), «Наименьшее общее кратное» (170390) помогут вам вспомнить некоторые алгоритмы, изученные на уроках русского языка и математики (http://sc.edu.ru/).

Пример 4. Некоторый алгоритм приводит к тому, что из одной цепочки символов получается новая цепочка следующим образом:

1. Вычисляется длина (в символах) исходной цепочки символов.
2. Если длина исходной цепочки нечётна, то к исходной цепочке справа приписывается цифра 1, иначе цепочка не изменяется.
3. Символы попарно меняются местами (первый — со вторым, третий — с четвёртым, пятый — с шестым и т. д).
4. Справа к полученной цепочке приписывается цифра 2.

Получившаяся таким образом цепочка является результатом работы алгоритма.

Так, если исходной была цепочка А#В, то результатом работы алгоритма будет цепочка #А1В2, а если исходной цепочкой была АБВ@, то результатом работы алгоритма будет цепочка БА@В2.

2.1.2. Исполнитель алгоритма

Каждый алгоритм предназначен для определённого исполнителя.

Исполнитель — это некоторый объект (человек, животное, техническое устройство), способный выполнять определённый набор команд.

Различают формальных и неформальных исполнителей. Формальный исполнитель одну и ту же команду всегда выполняет одинаково. Неформальный исполнитель может выполнять команду по-разному.

Рассмотрим более подробно множество формальных исполнителей. Формальные исполнители необычайно разнообразны, но для каждого из них можно указать следующие характеристики: круг решаемых задач (назначение), среду, систему команд и режим работы.

Круг решаемых задач. Каждый исполнитель создаётся для решения некоторого круга задач — построения цепочек символов, выполнения вычислений, построения рисунков на плоскости и т. д.

Среда исполнителя. Область, обстановку, условия, в которых действует исполнитель, принято называть средой данного исполнителя. Исходные данные и результаты любого алгоритма всегда принадлежат среде того исполнителя, для которого предназначен алгоритм.

Система команд исполнителя. Предписание исполнителю о выполнении отдельного законченного действия называется командой. Совокупность всех команд, которые могут быть выполнены некоторым исполнителем, образует систему команд данного исполнителя (СКИ). Алгоритм составляется с учётом возможностей конкретного исполнителя, иначе говоря, в системе команд исполнителя, который будет его выполнять.

Режимы работы исполнителя. Для большинства исполнителей предусмотрены режимы непосредственного управления и программного управления. В первом случае исполнитель ожидает команд от человека и каждую поступившую команду немедленно выполняет. Во втором случае исполнителю сначала задаётся полная последовательность команд (программа), а затем он выполняет все эти команды в автоматическом режиме. Ряд исполнителей работает только в одном из названных режимов.

Рассмотрим примеры исполнителей.

Пример 5. Исполнитель Черепашка перемещается на экране компьютера, оставляя след в виде линии.

Система команд Черепашки состоит из следующих команд:

1. Вперёд n (где n — целое число) — вызывает передвижение Черепашки на п шагов в направлении движения — в том направлении, куда развёрнуты её голова и корпус;
2. Направо m (где m — целое число) — вызывает изменение направления движения Черепашки на т градусов по часовой стрелке.
Запись Повтори k [<Команда1> <Команда2> ... <Командаn>] означает, что последовательность команд в скобках повторится k раз.

Подумайте, какая фигура появится на экране после выполнения Черепашкой следующего алгоритма.
Повтори 12 [Направо 45 Вперёд 20 Направо 45]

Пример 6. Система команд исполнителя Вычислитель состоит из двух команд, которым присвоены номера:

1 — вычти 1
2 — умножь на 3

Первая из них уменьшает число на 1, вторая увеличивает число в 3 раза. При записи алгоритмов для краткости указываются лишь номера команд. Например, алгоритм 21212 означает следующую последовательность команд:

умножь на 3
вычти 1
умножь на 3
вычти 1
умножь на 3

С помощью этого алгоритма число 1 будет преобразовано в 15:

((1 3 - 1) 3 - 1) 3 = 15.

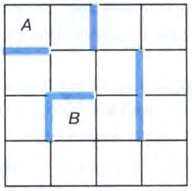
Пример 7. Исполнитель Робот действует на клетчатом поле, между соседними клетками которого могут стоять стены. Робот передвигается по клеткам поля и может выполнять следующие команды, которым присвоены номера:

1 — вверх
2 — вниз
3 — вправо
4 — влево

При выполнении каждой такой команды Робот перемещается в соседнюю клетку в указанном направлении. Если же в этом направлении между клетками стоит стена, то Робот разрушается.

Что произойдёт с Роботом, если он выполнит последовательность команд 32323 (здесь цифры обозначают номера команд), начав движение из клетки А? Какую последовательность команд следует выполнить Роботу, чтобы переместиться из клетки А в клетку В, не разрушившись от встречи со стенами?

При разработке алгоритма:

1) выделяются фигурирующие в задаче объекты, устанавливаются свойства объектов, отношения между объектами и возможные действия с объектами;
2) определяются исходные данные и требуемый результат;
3) определяется последовательность действий исполнителя, обеспечивающая переход от исходных данных к результату;
4) последовательность действий записывается с помощью команд, входящих в систему команд исполнителя.

Можно сказать, что алгоритм — модель деятельности исполнителя алгоритмов.

2.1.3. Свойства алгоритма

Не любая инструкция, последовательность предписаний или план действий может считаться алгоритмом. Каждый алгоритм обязательно обладает следующими свойствами: дискретность, понятность, определённость, результативность и массовость.

Свойство дискретности означает, что путь решения задачи разделён на отдельные шаги (действия). Каждому действию соответствует предписание (команда). Только выполнив одну команду, исполнитель может приступить к выполнению следующей команды.

Свойство понятности означает, что алгоритм состоит только из команд, входящих в систему команд исполнителя, т. е. из таких команд, которые исполнитель может воспринять и по которым может выполнить требуемые действия.

Свойство определённости означает, что в алгоритме нет команд, смысл которых может быть истолкован исполнителем неоднозначно; недопустимы ситуации, когда после выполнения очередной команды исполнителю неясно, какую команду выполнять следующей. Благодаря этому результат алгоритма однозначно определяется набором исходных данных: если алгоритм несколько раз применяется к одному и тому же набору исходных данных, то на выходе всегда получается один и тот же результат.

Свойство результативности означает, что алгоритм должен обеспечивать получение результата после конечного, возможно, очень большого, числа шагов. При этом результатом считается не только обусловленный постановкой задачи ответ, но и вывод о невозможности продолжения по какой-либо причине решения данной задачи.

Свойство массовости означает, что алгоритм должен обеспечивать возможность его применения для решения любой задачи из некоторого класса задач. Например, алгоритм нахождения корней квадратного уравнения должен быть применим к любому квадратному уравнению, алгоритм перехода улицы должен быть применим в любом месте улицы, алгоритм приготовления лекарства должен быть применим для приготовления любого его количества и т. д.

Пример 8. Рассмотрим один из методов нахождения всех простых чисел, не превышающих некоторое натуральное число n. Этот метод называется «решето Эратосфена» по имени предложившего его древнегреческого учёного Эратосфена (III в. до н. э.).

Для нахождения всех простых чисел, не больших заданного числа n, следуя методу Эратосфена, нужно выполнить следующие шаги:

1) выписать подряд все натуральные числа от 2 до n (2, 3, 4, ..., n);
2) заключить в рамку 2 — первое простое число;
3) вычеркнуть из списка все числа, делящиеся на последнее найденное простое число;
4) найти первое неотмеченное число (отмеченные числа — зачёркнутые числа или числа, заключённые в рамку) и заключить его в рамку — это будет очередное простое число;
5) повторять шаги 3 и 4 до тех пор, пока не останется неотмеченных чисел.

Более наглядное представление о методе нахождения простых чисел вы сможете получить с помощью размещённой в Единой коллекции цифровых образовательных ресурсов анимации «Решето Эратосфена» (180279).

Рассмотренная последовательность действий является алгоритмом, так как она удовлетворяет свойствам:

• дискретности — процесс нахождения простых чисел разбит на шаги;
• понятности — каждая команда понятна ученику 8 класса, выполняющему этот алгоритм;
• определённости — каждая команда трактуется и выполняется исполнителем однозначно; имеются указания об очерёдности выполнения команд;
• результативности — через некоторое число шагов достигается результат;
• массовости — последовательность действий применима для любого натурального n.

Рассмотренные свойства алгоритма позволяют дать более точное определение алгоритма.

Алгоритм — это предназначенное для конкретного исполнителя описание последовательности действий, приводящих от исходных данных к требуемому результату, которое обладает свойствами дискретности, понятности, определённости, результативности и массовости.

2.1.4. Возможность автоматизации деятельности человека

Разработка алгоритма — как правило, трудоёмкая задача, требующая от человека глубоких знаний, изобретательности и больших временных затрат.

Решение задачи по готовому алгоритму требует от исполнителя только строгого следования заданным предписаниям.

Пример 9. Из кучки, содержащей любое, большее трёх, количество каких-либо предметов, двое играющих по очереди берут по одному или по два предмета. Выигрывает тот, кто своим очередным ходом сможет забрать все оставшиеся предметы.

Рассмотрим алгоритм, следуя которому первый игрок наверняка обеспечит себе выигрыш.

1. Если число предметов в кучке кратно 3, то уступить ход противнику, иначе начать игру, взяв 1 или 2 предмета так, чтобы осталось количество предметов, кратное 3.
2. Своим очередным ходом каждый раз дополнять число предметов, взятых соперником, до 3 (число оставшихся предметов должно быть кратно 3).

Исполнитель может не вникать в смысл того, что он делает, и не рассуждать, почему он поступает так, а не иначе, т. е. он может действовать формально. Способность исполнителя действовать формально обеспечивает возможность автоматизации деятельности человека. Для этого:

1) процесс решения задачи представляется в виде последовательности простейших операций;
2) создаётся машина (автоматическое устройство), способная выполнять эти операции в последовательности, заданной в алгоритме;
3) человек освобождается от рутинной деятельности, выполнение алгоритма поручается автоматическому устройству.

САМОЕ ГЛАВНОЕ

Исполнитель — некоторый объект (человек, животное, техническое устройство), способный выполнять определённый набор команд.

Формальный исполнитель одну и ту же команду всегда выполняет одинаково. Для каждого формального исполнителя можно указать: круг решаемых задач, среду, систему команд и режим работы.

Алгоритм — предназначенное для конкретного исполнителя описание последовательности действий, приводящих от исходных данных к требуемому результату, которое обладает свойствами дискретности, понятности, определённости, результативности и массовости.

Способность исполнителя действовать формально обеспечивает возможность автоматизации деятельности человека.

Вопросы и задания

1. Ознакомьтесь с материалами презентации к параграфу, содержащейся в электронном приложении к учебнику. Дополняет ли презентация информацию, содержащуюся в тексте параграфа? Какими слайдами вы могли бы дополнить презентацию?

2. Что называют алгоритмом?

3. Подберите синонимы к слову «предписание».

4. Приведите примеры алгоритмов, изучаемых вами в школе.

5. Кто может быть исполнителем алгоритма?

6. Приведите пример формального исполнителя. Приведите пример, когда человек выступает в роли формального исполнителя.

7. От чего зависит круг решаемых задач исполнителя «компьютер»?

8. Рассмотрите в качестве исполнителя текстовый процессор, имеющийся на вашем компьютере. Охарактеризуйте круг решаемых этим исполнителем задач и его среду.

9. Что такое команда, система команд исполнителя?

10. Какие команды должны быть у робота, выполняющего функции:

а) кассира в магазине;
б) дворника;
в) охранника?

11. Перечислите основные свойства алгоритма.

12. К чему может привести отсутствие какого-либо свойства у алгоритма? Приведите примеры.

13. В чём важность возможности формального исполнения алгоритма?

14. Последовательность чисел строится по следующему алгоритму: первые два числа последовательности принимаются равными 1; каждое следующее число последовательности принимается равным сумме двух предыдущих чисел. Запишите 10 первых членов этой последовательности. Выясните, как называется эта последовательность.

15. Некоторый алгоритм получает из одной цепочки символов новую цепочку следующим образом. Сначала записывается исходная цепочка символов, после нее записывается исходная цепочка символов в обратном порядке, затем записывается буква, следующая в русском алфавите за той буквой, которая в исходной цепочке стояла на последнем месте. Если в исходной цепочке на последнем месте стоит буква «Я», то в качестве следующей буквы записывается буква «А». Получившаяся цепочка является результатом работы алгоритма. Например, если исходная цепочка символов была «ДОМ», то результатом работы алгоритма будет цепочка «ДОММОДН». Дана цепочка символов «КОМ». Сколько букв «О» будет в цепочке символов, которая получится, если применить алгоритм к данной цепочке, а затем ещё раз применить алгоритм к результату его работы?

16. Найдите в сети Интернет анимацию шагов алгоритма Эратосфена. С помощью алгоритма Эратосфена найдите все простые числа, не превышающие 50.

17. Что будет результатом исполнения Черепашкой (см. пример 5) алгоритма?

Повтори 8 [Направо 45 Вперёд 45]

18. Запишите алгоритм для исполнителя Вычислитель (см. пример 6), содержащий не более 5 команд:

а) получения из числа 3 числа 16;
б) получения из числа 1 числа 25.

19. Система команд исполнителя Конструктор состоит из двух команд, которым присвоены номера:

1 — приписать 2
2 — разделить на 2

По первой из них к числу приписывается справа 2, по второй число делится на 2. Как будет преобразовано число 8, если исполнитель выполнит алгоритм 22212? Составьте алгоритм в системе команд этого исполнителя, по которому число 1 будет преобразовано в число 16 (в алгоритме должно быть не более 5 команд).

20. В какой клетке должен находиться исполнитель Робот (пример 7), чтобы после выполнения алгоритма 3241 в неё же и вернуться?

Свободное программное обеспечение:

система КуМир — Комплект учебных миров (скачать архив программы с сайта) или посетить страницу КуМир ((http://www.niisi.ru/kumir/)

Электронное приложение к уроку

Cкачать материалы урока