Урок 13
Информационное моделирование на компьютере
Содержание урока
Информационное моделирование на компьютере. Компьютерная математическая модель
Информационное моделирование на компьютере. Управление на основе моделей
Информационное моделирование на компьютере. Вопросы и задания
Объектно-информационные модели. Что такое объект
Объектно-информационные модели. Наследование
Объектно-информационные модели. Вопросы и задания
Дополнительный материал. Объектно-инофрмационное моделирование
Информационное моделирование на компьютере
Компьютерная математическая модель
Изучаемые вопросы:
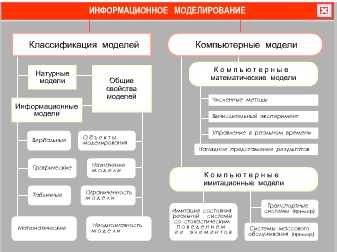
- Разновидности компьютерных моделей.
- Компьютерная математическая модель и вычислительный эксперимент.
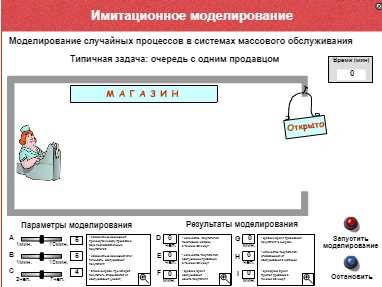
- Имитационное моделирование.
 |
 |
|
|
 |
 |
|
|
Основные темы параграфа:
- вычислительные возможности компьютера;
- для чего нужны математические модели;
- компьютерная математическая модель;
- что такое вычислительный эксперимент;
- управление на основе моделей;
- имитационное моделирование.
Вычислительные возможности компьютера
Современным инструментом для информационного моделирования является компьютер. Конечно, на компьютере можно писать тексты (строить вербальные модели), рисовать карты и схемы (графические модели), строить таблицы (табличные модели). Но при таком использовании компьютера в моделировании его возможности проявляются не в полной мере.
Для моделирования на компьютере главной является его способность к быстрому счету. Современные компьютеры считают со скоростями в сотни тысяч, миллионы и даже миллиарды операций в секунду.
Учитывая, что расчеты производятся над многозначными числами (10-20 десятичных цифр), вычислительные возможности компьютера феноменальны. Эти возможности проявляются, прежде всего, при компьютерном математическом моделировании.
Для чего нужны математические модели
Многие процессы, происходящие в природе, технике, экономических и социальных системах, описываются сложными математическими соотношениями. Это могут быть уравнения, системы уравнений, системы неравенств и пр., которые являются математическими моделями описываемых процессов.
Математическая модель — это описание моделируемого процесса на языке математики.
В прежние времена, до появления ЭВМ, ученые стремились создавать такие математические модели, которые можно было бы просчитать вручную или с помощью несложных вычислительных механизмов. Поэтому математические модели были относительно простыми. Но простая модель не всегда хорошо описывает процесс. Ошибка расчетов по такой модели может быть слишком большой и полностью обесценить результат.
Еще в XVIII-XIX веках ученые-математики начали изобретать методы решения таких математических задач, которые не удавалось решить точно, аналитически. Например, вы знаете, что квадратное уравнение всегда можно решить точно, а вот кубическое — уже не всегда. Такие методы называются численными методами. Они сводят решение любой задачи к последовательности арифметических операций. Но эта цепочка арифметических вычислений может быть очень длинной. И чем точнее мы хотим получить решение, тем она длиннее.
Может оказаться, что для решения сложной задачи численным методом ученому потребуется вся жизнь. А может и этого не хватить! И какой смысл, например, начинать расчет прогноза погоды на завтрашний день, если для этого потребуется несколько лет работы?
Компьютерная математическая модель
Появление компьютеров сняло эти проблемы. Стало возможным проводить расчеты сложных математических моделей за приемлемое время. Например, рассчитать погоду на завтрашний день до его наступления. Ученые перестали себя ограничивать в сложности создаваемых математических моделей, полагаясь на быстродействие компьютеров.
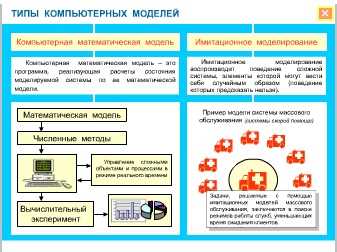
Компьютерная математическая модель — это программа, реализующая расчеты состояния моделируемой системы по ее математической модели.
Что такое вычислительный эксперимент
Использование компьютерной математической модели для исследования поведения объекта моделирования называется вычислительным экспериментом. Говорят также: численный эксперимент.
Вычислительный эксперимент в некоторых случаях может заменить реальный физический эксперимент.
Впечатляющий пример использования такой возможности — прекращение испытаний ядерного оружия, которые сопровождались значительным экологическим ущербом. Благодаря очень точным математическим моделям и мощным компьютерам стало возможно просчитать все последствия, к которым приводит изменение в конструкции ядерной бомбы. Образно говоря, удалось «взорвать бомбу» внутри компьютера, ничего не разрушив.
Важным свойством компьютерных математических моделей является возможность визуализации результатов расчетов. Этим целям служит использование компьютерной графики.
Представление результатов в наглядном виде — важнейшее условие для их лучшего понимания. Например, результаты расчетов распределения температуры в некотором объекте можно представить в виде его разноцветного изображения: участки с самой высокой температурой окрасить в красный цвет, а с самой холодной — в синий. Участки с промежуточными значениями температуры окрашиваются в цвета спектра, равномерно переходящие от красного к синему (рис. 2.7).
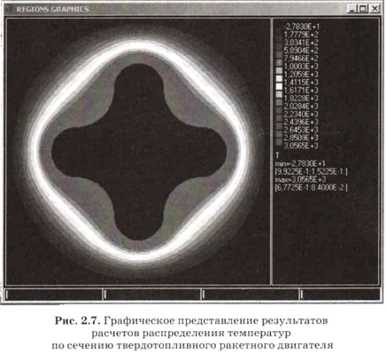
Для изображения изменяющихся со временем (динамических) результатов используют графическую анимацию.
Компьютерная графика позволяет человеку в процессе проведения численного эксперимента «заглянуть» в недоступные места исследуемого объекта. Можно получить изображение любого сечения объекта сложной формы с отображением рассчитываемых характеристик: температурных полей, давления и пр. В реальном физическом эксперименте такое можно сделать далеко не всегда. Например, невозможно выполнить измерения внутри работающей доменной печи или внутри звезды. А на модели это сделать можно.
