Урок 20
Условия поиска информации,
простые логические выражения
Основы логики:
логические величины и формулы
Изучаемые вопросы:
- Понятие логического выражения.
- Операции отношения.
- Запросы на выборку с использованием простых логических выражений.
Основные темы:
- формальная логика и алгебра логики;
- логические величины, операции, формулы;
- таблица истинности.
Содержание урока
Логические операции
Логические операции
Логические величины
Алгебра логики оперирует с логическими величинами, которые принимают всего два значения: «истина» или «ложь». Следовательно, каждая такая величина может быть сопоставлена некоторому высказыванию, иднако алгебра логики — это формализованная математическая дисциплина, поэтому логическая величина не должна обязательно иметь конкретный содержательный смысл.
Как принято в алгебре чисел, в алгебре логики логические величины могут быть константами и переменными. Логические константы обозначаются либо словами ИСТИНА и ЛОЖЬ, либо по-английски TRUE, FALSE. Логические переменные обозначаются символическими (буквенными) именами: X, A, Z, D2 и т. п. Алгебра чисел работает на числовом множестве значений величин, которыми она оперирует. Множество чисел бесконечно. Алгебра логики работает на множестве, состоящем всего из двух значений: «истина» и «ложь». В этом смысле она проще алгебры чисел.
Логические операции
В алгебре логики имеются шесть логических операций. Они называются так:
1) отрицание (инверсия);
2) логическое умножение (конъюнкция);
3) логическое сложение (дизъюнкция);
4) разделительная дизъюнкция;
5) следование (импликация);
6) эквивалентность.
Первые три являются основными логическими операциями. Три последние могут быть выражены через основные операции. Поэтому в дальнейшем мы будем рассматривать только три операции: отрицание, логическое умножение и логическое сложение.
Правила выполнения логических операций нетрудно запомнить.
Операция отрицания изменяет значение логической величины на противоположное: не истина = ложь; не ложь = истина. Для обозначения операции отрицания используют частицу «не».
Отрицание — одноместная операция, т. е. она применяется к одному операнду. Операции логического умножения и логического сложения — двухместные.
Результатом логического умножения будет ИСТИНА, только если истинны значения обоих операндов: истина и истина = истина. Во всех остальных случаях результатом будет ЛОЖЬ. Для обозначения операции логического умножения используют связку «и».
Результат логического сложения — ЛОЖЬ только в том случае, если оба операнда имеют значение ЛОЖЬ: ложь или ложь = ложь. Во всех остальных случаях будет ИСТИНА. Для обозначения операции логического сложения используют связку «или».
Таблица на рис. 3.1 иллюстрирует вед» правила выполнения трех логических операций. Такую таблицу называют таблицей истинности. В ней буквами А и Б обозначены логические операнды. Величина ИСТИНА обозначена цифрой 1, логическая величина ЛОЖЬ цифрой 0.
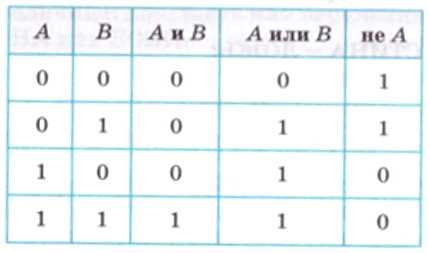
Рис. 3.1. Таблица истинности
