Урок 20
Условия поиска информации,
простые логические выражения
Основы логики:
логические величины и формулы
Изучаемые вопросы:
- Понятие логического выражения.
- Операции отношения.
- Запросы на выборку с использованием простых логических выражений.
Основные темы:
- формальная логика и алгебра логики;
- логические величины, операции, формулы;
- таблица истинности.
Содержание урока
Логические формулы
Логические формулы
В алгебре чисел существует понятие алгебраического выражения или формулы. Вот пример алгебраического выражения: (а + Ь)2. Аналогом этого понятия в алгебре логики является понятие логического выражения или логической формулы.
Логическая формула может включать в себя логические константы, логические переменные, знаки логических операций. Для влияния на последовательность выполнения операций в логических формулах могут использоваться скобки. Пример логической формулы: не (А и В) или С. Здесь А, В, С — логические величины.
При записи логических формул следует учитывать старшинство логических операций. Логические операции в порядке убывания старшинства (еще говорят - ранга) располагаются так:
1) отрицание (не);
2) конъюнкция (и);
3) дизъюнкция (или).
Как и в числовой алгебре, в первую очередь выполняются операции более высокого ранга.
Пример 1. Для следующих логических формул цифрами сверху указана последовательность выполнения операций:
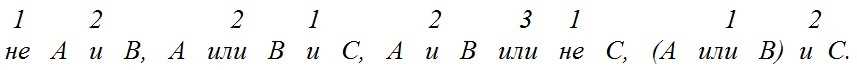
Пример 2. Вычислим значение логической формулы
не (А и В) или С
при следующих значениях переменных: А = ЛОЖЬ, В = ИСТИНА С - ЛОЖЬ.
Порядок вычисления такой: сначала выполняется операция в скобках (и), затем отрицание (не) и последней операция логического сложения (или):
1) ЛОЖЬ и ИСТИНА = ЛОЖЬ;
2) не ЛОЖЬ = ИСТИНА;
3) ИСТИНА или ЛОЖЬ = ИСТИНА.
Следовательно, в результате получено значение ИСТИНА.
Чтобы получить всевозможные значения логической формулы, нужно для нее построить таблицу истинности. В таблице истинности перебираются все варианты значений переменных, входящих в формулу, и для каждого варианта вычисляется результат. Поскольку каждая переменная может принимать только два значения, то число строк в таблице истинности для формулы, содержащей п переменных, будет равно 2n.
Пример 3. Получим таблицу истинности для рассмотренной выше формулы не (А и В) или С. Поскольку она содержит 3 переменные, то таблица будет иметь 8 строк 23 = 8).
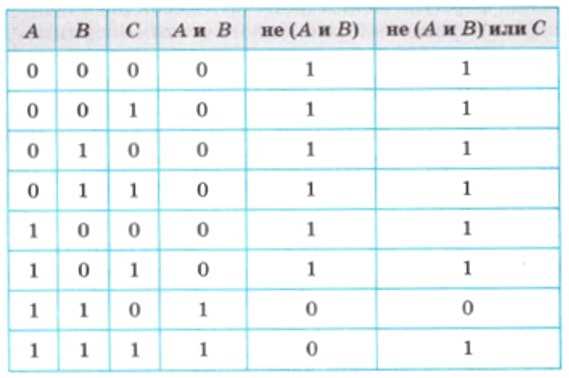
Столбцы слева направо расположены в порядке выполняемых операций. Оказалось, что данная формула принимает значение ИСТИНА во всех случаях, кроме одного: А = ИСТИНА, В = ИСТИНА, С = ЛОЖЬ. В этом случае ее значение — ЛОЖЬ.


