Урок 5
Вероятностный (содержательный) подход к измерению количества информации
§ 1.3. Количество информации
Содержание урока
1.3.1. Количество информации как мера уменьшения неопределенности знания
1.3.2. Определение количества информации
1.3.2. Определение количества информации
Определение количества информационных сообщений. По формуле (1.1) можно легко определить количество возможных информационных сообщений, если известно количество информации. Например, пусть на экзамене студент берет экзаменационный билет, и учитель сообщает ему, что зрительное информационное сообщение о номере билета несет 5 битов информации. Если вы хотите определить количество экзаменационных билетов, то достаточно определить количество возможных информационных сообщений об их номерах по формуле (1.1):
N = 25 = 32.
Таким образом, количество экзаменационных билетов равно 32.
Определение количества информации. Наоборот, если известно возможное количество информационных сообщений N, то для определения количества информации, которое несет сообщение, необходимо решить уравнение (1.1) относительно I.
Представьте себе, что вы управляете движением робота и можете задавать направление его движения с помощью информационных сообщений: «север», «северо-восток», «восток», «юго-восток», «юг», «юго-запад», «запад» и «северо-запад» (рис. 1.12). Какое количество информации будет получать робот после каждого сообщения?
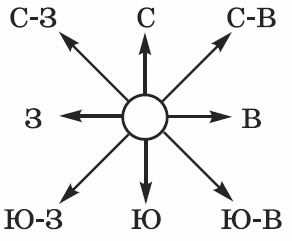
Рис. 1.12. Управление роботом с использованием информационных сообщений
Всего возможных информационных сообщений 8, поэтому формула (1.1) принимает вид уравнения относительно I:
8 = 2I.
Разложим стоящее в левой части уравнения число 8 на сомножители, равные 2, и представим его в степенной форме:
8 = 2 • 2 • 2 = 23.
Получим степенное уравнение, из которого необходимо найти неизвестное I:
23 = 2I.
Равенство левой и правой частей уравнения справедливо, если равны показатели степени числа 2. Таким образом, I = 3 бита, т. е. количество информации, которое несет роботу каждое информационное сообщение, равно 3 битам.
Задания для самостоятельного выполнения
1.5. Задание с выборочным ответом. Производится бросание симметричной четырехгранной пирамидки. Какое количество информации мы получаем в зрительном сообщении о ее падении на одну из граней?
1) 1 бит
2) 2 бита
3)4 бита
4) 1 байт
1.6. Задание с кратким ответом. Из непрозрачного мешочка вынимают шарики с номерами, и известно, что информационное сообщение о номере шарика несет 5 битов информации. Определите количество шариков в мешочке.
1.7. Задание с развернутым ответом. Какое количество информации при игре в крестики-нолики на поле размером 4x4 клетки получит второй игрок после первого хода первого игрока?
Cкачать материалы урока
