Урок 18
Кодирование числовой информации. Системы счисления
§ 4.1. Кодирование числовой информации
Содержание урока
4.1.1. Представление числовой информации с помощью систем счисления
Лабораторная работа № 10 «Учимся кодировать числовую информацию в разных системах счисления»
4.1.1. Представление числовой информации с помощью систем счисления
Для записи информации о количестве объектов используются числа. Числа записываются с использованием особых знаковых систем, которые называются системами счисления. Алфавит системы счисления состоит из знаков, которые называются цифрами.
Система счисления — это знаковая система, в которой числа записываются по определенным правилам с помощью знаков некоторого алфавита, называемых цифрами.
Все системы счисления делятся на две большие группы: позиционные и непозиционные системы. В позиционных системах счисления количественное значение цифры зависит от ее положения в числе, а в непозиционных — не зависит.
Непозиционные системы счисления. Как только люди начали считать, у них появилась потребность в записи чисел. Находки археологов на стоянках первобытных людей свидетельствуют о том, что первоначально количество предметов отображали равным количеством каких-либо значков: зарубок, черточек, точек.
Такая система записи чисел называется единичной, так как любое число в ней образуется путем повторения одного знака, символизирующего единицу (рис. 4.1). Единичной системой счисления пользуются малыши, показывая на пальцах свой возраст или используя для этого счетные палочки.
Примером непозиционной системы, которая сохранилась до наших дней, может служить римская система счисления, которая начала применяться более двух с половиной тысяч лет назад в Древнем Риме.
Рис. 4.1. Единичная система счисления
В основе римской системы счисления лежат знаки I (один палец) для числа 1, V (раскрытая ладонь) для числа 5, X (две сложенные ладони) для 10, а для обозначения чисел 100, 500 и 1000 используются латинские буквы С, D и М (рис. 4.2).
Рис. 4.2. Римская система счисления
В римской системе счисления значение цифры не зависит от ее положения в числе. Например, в римском числе XXX (30) цифра X встречается трижды и в каждом случае обозначает одну и ту же величину — число 10, три раза по 10 в сумме дают 30.
Чтобы записать число в римской системе счисления, необходимо разложить его на сумму тысяч, полутысяч, сотен, полусотен, десятков, пятерок, единиц. Например, десятичное число 28 представляется следующим образом:
10 + 10 + 5 + 1 + 1 + 1 = XXVIII
(два десятка, пятерка, три единицы).
При записи чисел в римской системе счисления применяется правило: каждый меньший знак, поставленный справа от большего, прибавляется к большему знаку, а каждый меньший знак, поставленный слева от большего, вычитается из большего знака.
Например, римское число IX обозначает 9 (-1 + 10), а XI обозначает 11 (10 + 1). Например, число 99 имеет следующее представление в римской системе счисления:
XCIX = -10 + 100 -1 + 10
Позиционные системы счисления. Каждая позиционная система счисления имеет определенный алфавит цифр и основание. Основание системы равно количеству цифр (знаков) в ее алфавите.
В позиционных системах счисления количественное значение цифры зависит от ее позиции в числе. Позиция цифры в числе называется разрядом. Разряды числа возрастают справа налево, от младших разрядов к старшим, причем значения цифр в соседних разрядах числа различаются в количество раз, равное основанию системы.
В настоящее время наиболее распространенной позиционной системой счисления является десятичная система. В информатике широко используются двоичная, восьмеричная и шестнадцатеричная системы счисления.
Десятичная система счисления (табл. 4.1). В десятичной системе счисления цифра в крайней справа позиции обозначает количество единиц, цифра, смещенная на одну позицию влево, обозначает количество десятков, еще левее — сотен, затем тысяч и т. д. Рассмотрим в качестве примера десятичное число 555. Цифра 5 встречается в числе трижды, причем самая правая обозначает пять единиц, вторая справа — пять десятков и, наконец, третья — пять сотен.
Выше десятичное число 555 было записано в привычной для нас свернутой форме. Мы настолько привыкли к такой форме записи, что уже не замечаем, как в уме умножаем цифры числа на число 10 в различных степенях, где 10 является основанием десятичной системы счисления.
В развернутой форме записи числа умножение цифр числа на основание производится в явной форме. Так, в развернутой форме запись числа 555 в десятичной системе будет выглядеть следующим образом:
55510 = 5 • 102 + 5 • 101 + 5 • 100.
Для записи десятичных дробей используются разряды с отрицательными значениями степеней основания. Например, число 555,55 в развернутой форме будет записано следующим образом:
555,5510 = 5 • 102 + 5 • 101 + 5 • 100 + 5 • 10-1 + 5 • 10-2.
Умножение или деление десятичного числа на 10 (величину основания) приводит к перемещению запятой, отделяющей целую часть от дробной, на один разряд соответственно вправо или влево. Например:
555,5510 • 10 = 5555,510;
555,5510 : 10 = 55,55510.
Двоичная система счисления (см. табл. 4.1). Числа в двоичной системе в развернутой форме записываются в виде суммы основания 2 в различных степенях с коэффициентами, в качестве которых выступают цифры 0 или 1.
Например, развернутая запись двоичного числа выглядит следующим образом:
A2 = 1 • 22 + 0 • 21 + 1 • 20 + 0 • 2-1 + 1 • 2-2, это же число в свернутой форме:
A2 = 101,012.
Умножение или деление двоичного числа на 2 (величину основания) приводит к перемещению запятой, отделяющей целую часть от дробной на один разряд соответственно вправо или влево. Например:
101,012 • 2 = 1010,12;
101,012 : 2 = 10,1012.
Восьмеричная система счисления (см. табл. 4.1). В восьмеричной системе основание равно 8 и алфавит состоит из восьми цифр {0, 1, 2, 3, 4, 5, 6, 7}. Запишем восьмеричное число в свернутой и развернутой формах:
778 = 7 • 81 + 7 • 80.
Шестнадцатеричная система счисления (см. табл. 4.1). В шестнадцатеричной системе основание равно 16 и алфавит состоит из шестнадцати цифр {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, А, В, С, D, Е, F}, причем первые десять цифр имеют общепринятое обозначение, а для записи остальных цифр со значениями 10, 11, 12, 13, 14, 15 используются первые шесть букв латинского алфавита. Запишем шестнадцатеричное число в свернутой и развернутой формах:
ABCDEF16= А • 165 + В • 164 + С • 163 + D • 162 + Е • 161 + F • 160 = 10 • 165 + 11 • 164 + 12 • 163 + 13 • 162+ 14 • 161 + 15 • 160.
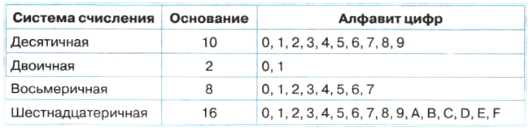
Таблица 4.1. Позиционные системы счисления
Первая позиционная система счисления была придумана еще в древнем Вавилоне, причем вавилонская нумерация была шестидесятеричной, т. е. в ней использовалось шестьдесят цифр! Интересно, что до сих пор при измерении времени мы используем основание, равное 60 (в 1 минуте содержится 60 секунд, а в 1 часе — 60 минут).
В XIX веке довольно широкое распространение получила двенадцатеричная система счисления. До сих пор мы часто употребляем дюжину (число 12): в сутках две дюжины часов, круг содержит тридцать дюжин градусов и т. д.
Контрольные вопросы
1. Чем отличаются позиционные системы счисления от непозиционных?
2. Каково основание десятичной системы счисления? Двоичной системы счисления? Восьмеричной системы счисления? Шестнадцатеричной системы счисления?
3. Какие цифры входят в алфавит десятичной системы счисления? Двоичной системы счисления? Восьмеричной системы счисления? Шестнадцатеричной системы счисления?
4. Во сколько раз в позиционных системах счисления различаются значения цифр соседних разрядов числа?
5. Может ли в качестве цифры в системе счисления использоваться символ буквы?
Задания для самостоятельного выполнения
4.1. Задание с кратким ответом. Запишите числа 3,1410 и 10,12 в развернутой форме.
4.2. Задание с кратким ответом. Во сколько раз увеличатся числа 10,110 и 10,12 при переносе запятой на один знак вправо?
4.3. Задание с кратким ответом. При переносе запятой на два знака вправо число 11,11х увеличилось в 4 раза. Чему равно основание х системы счисления?
4.4. Задание с кратким ответом. Какое минимальное основание может иметь система счисления, если в ней записано число 11? Число 99?
4.5. Задание с кратким ответом. Запишите год, месяц и число своего рождения с помощью римских цифр.
Cкачать материалы урока
