Урок 9
§13. Модели и моделирование
Содержание урока
Адекватность моделей
Практическая работа № 9 «Броуновское движение»
Адекватность моделей
Итак, при моделировании мы заменяем один объект (объект - оригинал) другим. Поэтому всегда возникает вопрос, можно ли верить полученным результатам. Иначе говоря, будет ли оригинал вести себя так же, как и модель?
 Адекватность модели — это совпадение существенных свойств модели и оригинала в рассматриваемой задаче.
Адекватность модели — это совпадение существенных свойств модели и оригинала в рассматриваемой задаче.
Используя дополнительные источники, выясните, от какого иностранного слова произошло слово «адекватный».
Адекватность означает, что результаты моделирования:
• не противоречат выводам теории, например законам сохранения (вещества, энергии и т. п.);
• подтверждаются экспериментом с оригиналом.
Таким образом, адекватность модели окончательно можно доказать только экспериментом: если результаты нашего моделирования близки к наблюдаемым на практике, это означает, что модель адекватна.
Для того чтобы вычислить ошибку моделирования, нужно модуль разности между результатом моделирования X и результатом эксперимента X* разделить на результат эксперимента и умножить на 100%:
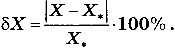
Величина «дельта икс» - называется относительной ошибкой. На практике модель обычно считается адекватной, если относительная ошибка не превышает 10%.
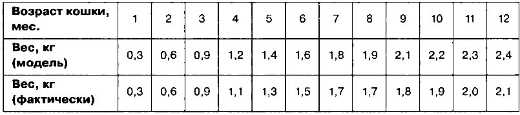
Феофан построил математическую модель, которая позволяет прогнозировать изменение веса кошки. Для какого периода времени модель Феофана адекватна?
Нужно понимать, что любая модель отличается от оригинала, поэтому она может быть адекватна только при определённых условиях — в той задаче, для решения которой она создавалась. Например, модель деления амёб (через некоторый интервал времени каждая амёба делится надвое) адекватна только при малом количестве амёб и небольших интервалах наблюдения, иначе амёбы заполнили бы всё пространство.
Во многих случаях результаты моделирования — это некоторые числа, измеренные или рассчитанные по результатам эксперимента с моделью. Это могут быть, например, сила, расстояние, скорость, ускорение, давление и др. Чаще всего эти величины для модели и оригинала будут различаться, поэтому нужно уметь пересчитывать «модельные» данные в соответствующие значения для оригинала. Этими вопросами занимается теория подобия. Простейший пример — работа с картой. Расстояние, измеренное по карте, нужно умножить на масштабный множитель, тогда получится соответствующее расстояние на реальной местности.
Следующая страница  Выводы
Выводы

