Урок 13
§8. Логика и компьютер

Содержание урока

Что такое высказывание?

Простые и сложные высказывания

Операция НЕ

Операция И

Операция ИЛИ

Выводы

Вопросы и задания

Операция И

Из двух простых высказываний А и В (например, А = Сейчас идёт дождь, В = Форточка открыта) можно составить сложное высказывание А и B. Высказывание А и B истинно в том и только в том случае, когда оба высказывания, А и B, истинны одновременно.

Для понимания операции И можно представить себе простую схему, в которой для включения лампочки используются два выключателя, соединённых последовательно (рис. 2.2).

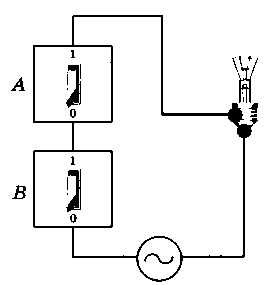
Рис. 2.2

Чтобы лампочка загорелась, нужно обязательно включить оба выключателя. Вместе с тем, чтобы выключить лампочку, достаточно выключить любой из них.

Операция И (в отличие от НЕ) выполняется с двумя логическими значениями. В алгоритмическом языке системы КуМир операция И обозначается словом и, а в Паскале — словом and.

Используя дополнительные источники, найдите другие обозначения операции И.

В таблице истинности операции И будет уже не один столбец с исходными данными, а два, мы обозначим исходные данные как А и B. Число строк также выросло, с 2 до 4, поскольку с помощью 2 бит можно записать 4 разных комбинации значений двух переменных: 00, 01, 10 и 11. Как следует из определения операции И, в последнем столбце будет всего одна единица, для варианта А = B = 1 (оба высказывания, А и Б, истинны одновременно) — рис. 2.3.

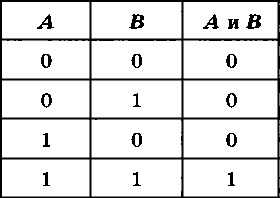
Рис. 2.3

Из значений А и В в каждой строке этой таблицы составьте двоичное число и запишите его в десятичной системе счисления. Почему строки в таблице расположены именно так?

Легко проверить, что этот результат можно получить «обычным» умножением А на В, поэтому операцию И называют логическим умножением. Она часто обозначается знаком умножения (точкой): А • В.

С точки зрения обычной математики, эта операция выбирает наименьшее из исходных значений. Математики используют ещё одно название операции И — конъюнкция.

Используя дополнительные источники, выясните, от какого слова произошло слово «конъюнкция» и что оно обозначает.

С помощью таблицы истинности можно упрощать логические выражения. Например, рассмотрим выражение А и 1. По таблице истинности на рис. 2.3 получаем:

при А = 0:     А и 1 = 0 и 1 = 0

при А = 1:     А и 1 = 1 и 1 = 1.

Можно заметить, что в любом случае результат совпадает с А, поэтому А и 1 = А.

Используя таблицу истинности операции И, упростите выражения: а) А и 0;      б) А и А;      в) А и (не А).

Следующая страница Операция ИЛИ

Cкачать материалы урока