Уроки 27 - 28
§17. Графы
Содержание урока
Связный граф
Связный граф
В графе на рис. 3.17, б все вершины связаны: между любой парой вершин существует путь — последовательность вершин, в которой каждая следующая связана ребром с предыдущей. Такой граф называется связным.
Связный граф — это граф, между любыми вершинами которого существует путь.
Теперь представьте себе, что дороги Васюки-Солнцево, Васюки-Грибное и Грибное-Ягодное завалило снегом (или размыло дождём) так, что по ним ни пройти, ни проехать (рис. 3.21).
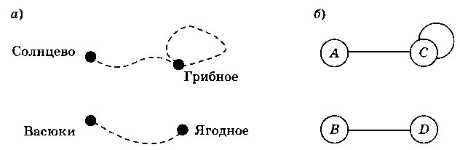
Рис. 3.21
Эту схему тоже можно считать графом (она соответствует определению), но в таком графе есть две несвязанные части, каждая из которых — связный граф. Такие части называют компонентами связности.
Постройте матрицу смежности графа, изображённого на рис. 3.21.
Граф имеет 4 вершины и две компоненты связности. Какое наибольшее количество рёбер может быть в этом графе, если в нём нет петель? Нарисуйте этот граф.
Вспоминая материал предыдущего параграфа, можно сделать вывод, что дерево — это частный случай связного графа. Но у него есть одно важное свойство — в дереве нет замкнутых путей — циклов, т. е. путей, которые начинаются и заканчиваются в одной и той же вершине.
Найдите все циклы в графе на рис. 3.17.
Дерево — это связный граф, в котором нет циклов.
Следующая страница 
Взвешенный граф
Cкачать материалы урока
