Урок 37
§21. Матрицы (двумерные массивы)

Содержание урока

Что такое матрицы?

Обработка элементов матрицы

Выводы

Вопросы и задания

Практическая работа № 18 «Матрицы»

Обработка элементов матрицы

Покажем, как можно обработать (например, сложить) некоторые элементы квадратной матрицы А, содержащей N строк и N столбцов.

Для квадратной матрицы используют понятия «главная диагональ» (серые клетки на рис. 4.4, а) и «побочная диагональ» (рис. 4.4, б). На рис. 4.4, в выделены главная диагональ и все элементы под ней.

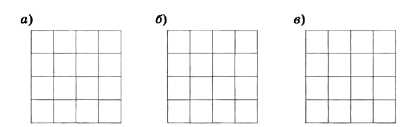
Рис. 4.4

Главная диагональ — это элементы А[1,1], А [ 2, 2 ], ...f A [N, N], т. е. элементы, у которых номер строки равен номеру столбца. Для перебора этих элементов нужен один цикл:

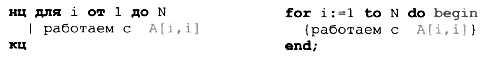
Элементы побочной диагонали — это A[1,N], А [2, N-1], ..., A[N,1]. Заметим, что сумма номеров строки и столбца для каждого элемента равна N+1, поэтому получаем такой цикл перебора:

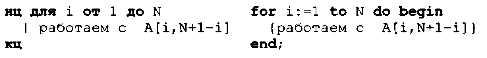
Запишите в тетради фрагмент программы, который вычисляет сумму всех элементов главной диагонали квадратной матрицы в переменной s.

Запишите в тетради фрагмент программы, который вычисляет количество ненулевых элементов побочной диагонали матрицы в переменной к.

В случае в) (обработка всех элементов на главной диагонали и под ней) нужен вложенный цикл: номер строки будет меняться от 1 до N, а номер столбца для каждой строки i — от 1 до i:

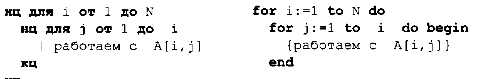
Запишите в тетради фрагмент программы, который вычисляет среднее арифметическое элементов матрицы, находящихся на главной диагонали и под ней.

Чтобы переставить строки или столбцы, достаточно одного цикла. Например, переставим строки 2 и 4, используя вспомогательную целую переменную с:

Запишите в тетради фрагмент программы, который переставляет столбцы матрицы с индексами 3 и 4.

Следующая страница Выводы

Cкачать материалы урока