Урок 39
§22. Сложность алгоритмов

Содержание урока

Как сравнивать алгоритмы?

Примеры вычисления сложности

Что такое асимптотическая сложность?

Выводы

Вопросы и задания

Примеры вычисления сложности

Рассмотрим алгоритмы выполнения различных операций с массивом А длины N, который может быть объявлен в программе так:

целтаб А[1:N]                var A: array[1..N] of integer;

Пример 1. Вычислить сумму значений первых трёх элементов массива (при N ≥ 3).

Решение этой задачи содержит всего один оператор:

Sum:=А[1]+А[2]+А[3];

Этот алгоритм включает две операции сложения и одну операцию записи значения в память, поэтому его сложность T(N) = 3 не зависит от размера массива вообще.

Вычислите количество операций (считая сравнения и присваивание значений переменным) при выполнении фрагмента программы:

Пример 2. Вычислить сумму значений всех элементов массива.

В этой задаче уже не обойтись без цикла:

Здесь выполняется N операций сложения и N + 1 операция записи в память, поэтому его сложность T(N) = 2N + 1 возрастает линейно с увеличением длины массива.

Вычислите количество операций при выполнении фрагмента программы:

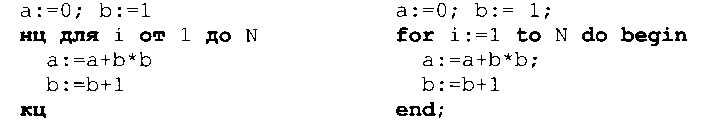
Пример 3. Отсортировать все элементы массива по возрастанию методом выбора. Напомним, что метод выбора предполагает поиск на каждом шаге минимального из оставшихся неупорядоченных значений (здесь i, j, nMin и с — целочисленные переменные):

Подсчитаем отдельно количество сравнений и количество перестановок. Количество сравнений элементов массива не зависит от данных и определяется числом шагов внутреннего цикла:

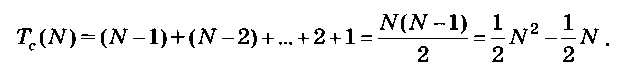
Здесь использована формула для суммы первых N - 1 членов арифметической прогрессии.

На каждом шаге внешнего цикла происходит перестановка двух элементов, общее количество перестановок равно Т_n( N) = N -1, т. е. сложность по перестановкам — линейная.

Определите количество операций при вычислении суммы значений элементов квадратной матрицы А размером N х N (здесь i, j и Sum — целочисленные переменные):

По результатам этих примеров можно сделать выводы:

• простой цикл, в котором количество шагов пропорционально N, — это алгоритм линейной сложности;
• вложенный цикл, в котором количество шагов внешнего и внутреннего цикла пропорционально N, — это алгоритм квадратичной сложности.

Следующая страница Что такое асимптотическая сложность?

Cкачать материалы урока