Урок 3
§1.2 Знаковые модели

1.2.1. Словесные модели

Словесные модели — это описания предметов, явлений, событий, процессов на естественных языках.

Например, гелиоцентрическая модель мира, которую предложил Коперник, словесно описывалась следующим образом:

• Земля вращается вокруг своей оси и вокруг Солнца;
• все планеты движутся по орбитам, центром которых является Солнце.

Множество словесных моделей содержится в ваших школьных учебниках: в учебнике истории представлены модели исторических событий, в учебнике географии — модели географических объектов и природных процессов, в учебнике биологии — модели объектов животного и растительного мира.

Произведения художественной литературы — это тоже модели, так как они фиксируют внимание читателя на определённых сторонах человеческой жизни. Анализируя литературное произведение, вы выделяете в нём объекты и их свойства, отношения между героями, связи между событиями, проводите параллели с другими произведениями и т. п. Самое непосредственное отношение к понятию модели имеет такой литературный жанр, как басня. Смысл этого жанра состоит в переносе отношений между людьми на отношения между вымышленными персонажами, например животными.

Такие особенности естественного языка, как многозначность, использование слов в прямом и переносном значении, синонимия, омонимия и т. п., придают человеческому общению выразительность, эмоциональность, красочность. Вместе с тем наличие этих особенностей делает естественный язык непригодным для создания информационных моделей во многих сферах профессиональной деятельности (например, в системах «человек — компьютер»).

1.2.2. Математические модели

Основным языком информационного моделирования в науке является язык математики.

Информационные модели, построенные с использованием математических понятий и формул, называются математическими моделями.

Язык математики представляет собой совокупность множества формальных языков; с некоторыми из них (алгебраическим, геометрическим) вы познакомились в школе, другие сможете узнать при дальнейшем обучении.

Язык алгебры позволяет формализовать функциональные зависимости между величинами, записав соотношения между количественными характеристиками объекта моделирования. В школьном курсе физики рассматривается много функциональных зависимостей, которые представляют собой математические модели изучаемых явлений или процессов.

Пример 1. Зависимость координаты тела от времени при прямолинейном равномерном движении имеет вид:

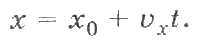
Изменение координаты тела х при прямолинейном равноускоренном движении в любой момент времени t выражается формулой:

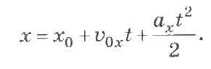
С помощью языка алгебры логики строятся логические модели — формализуются (записываются в виде логических выражений) простые и составные высказывания, выраженные на естественном языке. Путём построения логических моделей удаётся решать логические задачи, создавать логические модели устройств и т. д.

Пример 2. Рассмотрите электрические схемы (рис. 1.3).

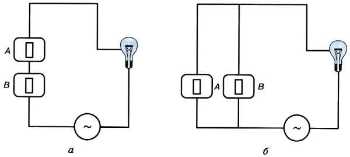
Рис. 1.3. Электрические схемы: а — последовательного и б — параллельного соединения переключателей

На них изображены известные вам из курса физики последовательное и параллельное соединения переключателей. В первом случае, чтобы лампочка загорелась, должны быть включены оба переключателя. Во втором случае достаточно, чтобы был включён один из переключателей.

Можно провести аналогию между элементами электрических схем и объектами и операциями алгебры логики:

Спроектируем электрическую цепь, показывающую итог тайного голосования комиссии в составе председателя и двух рядовых членов. При голосовании «за» каждый член комиссии нажимает кнопку. Предложение считается принятым, если члены комиссии проголосуют за него единогласно либо если свои голоса «за» отдадут председатель и один из рядовых членов комиссии. В этих случаях загорается лампочка.

Решение

Пусть голосу председателя соответствует переключатель А, голосам рядовых членов — переключатели В и С. Тогда F(A, В, C) = A & B & C ∨ A & B ∨ A & C.

Упростим полученное логическое выражение:

F(A, В, C) = A & B & (C ∨ 1) ∨ A & C = A & B & 1 ∨ A & C = A & B ∨ A & C = A & (B ∨ С).

Мы получили логическую модель, позволяющую построить схему проектируемой электрической цепи (рис. 1.4).

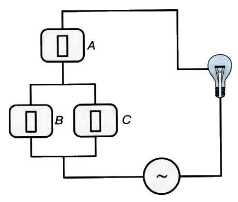
Рис. 1.4. Схема электрической цепи

1.2.3. Компьютерные математические модели

Многие процессы, происходящие в окружающем нас мире, описываются очень сложными математическими соотношениями (уравнениями, неравенствами, системами уравнений и неравенств). До появления компьютеров, обладающих высокой скоростью вычислений, у человека не было возможности проводить соответствующие вычисления, на счёт «вручную» уходило очень много времени.

В настоящее время многие сложные математические модели могут быть реализованы ¹ на компьютере. При этом используются такие средства, как:

• системы программирования;
• электронные таблицы;
• специализированные математические пакеты и программные средства для моделирования.

---

¹ Реализация математической модели — это расчёт состояния (выходных параметров) моделируемой системы по формулам, связывающим её входные и выходные параметры.

Математические модели, реализованные с помощью систем программирования, электронных таблиц, специализированных математических пакетов и программных средств для моделирования, называются компьютерными математическими моделями.

Средства компьютерной графики позволяют визуализировать результаты расчётов, получаемых в процессе работы с компьютерными моделями.

С помощью ресурса «Демонстрационная математическая модель» (119324) вы сможете смоделировать полёт снаряда, выпущенного из пушки при различных исходных данных (http://sc.edu.ru/).

Особый интерес для компьютерного математического моделирования представляют сложные системы, элементы которых могут вести себя случайным образом. Примерами таких систем являются многочисленные системы массового обслуживания: билетные кассы, торговые предприятия, ремонтные мастерские, служба «Скорой помощи», транспортные потоки на городских дорогах и многие другие модели. Многим знакома ситуация, когда, придя в кассу, магазин, парикмахерскую, мы застаём там очередь. Приходится либо вставать в очередь и какое-то время ждать, либо уходить, т. е. покидать систему необслуженным. Возможны случаи, когда заявок на обслуживание в системе мало или совсем нет; в этом случае она работает с недогрузкой или простаивает. В системах массового обслуживания количество заявок на обслуживание, время ожидания и точное время выполнения заявки заранее предсказать нельзя — это случайные величины.

Имитационные модели воспроизводят поведение сложных систем, элементы которых могут вести себя случайным образом.

Имитационное моделирование — это искусственный эксперимент, при котором вместо проведения натурных испытаний с реальным оборудованием проводят опыты с помощью компьютерных моделей. Для получения необходимой информации осуществляется многократный «прогон» моделей со случайными исходными данными, генерируемыми компьютером. В результате образуется такой же набор данных, который можно было бы получить при проведении опытов на реальном оборудовании или в реальной системе. Однако имитационное моделирование на компьютере осуществляется гораздо быстрее и обходится значительно дешевле, чем натурные эксперименты.

С помощью ресурса «Демонстрационная имитационная модель» (119425) вы сможете смоделировать ситуацию в системе массового обслуживания — магазине (http://sc.edu.ru/).

САМОЕ ГЛАВНОЕ

Словесные модели — это описания предметов, явлений, событий, процессов на естественных языках.

Информационные модели, построенные с использованием математических понятий и формул, называются математическими моделями.

Математические модели, реализованные с помощью систем программирования, электронных таблиц, специализированных математических пакетов и программных средств для моделирования, называются компьютерными математическими моделями.

Имитационные модели воспроизводят поведение сложных систем, элементы которых могут вести себя случайным образом.

Вопросы и задания

1. Ознакомьтесь с материалами презентации к параграфу, содержащейся в электронном приложении к учебнику. Что вы можете сказать о формах представления информации в презентации и в учебнике? Какими слайдами вы могли бы дополнить презентацию?

2. Приведите 2-3 собственных примера словесных моделей, рассматриваемых на уроках истории, географии, биологии.

3. Вспомните басни И. А. Крылова: «Волк и Ягнёнок», «Ворона и Лисица», «Демьянова уха», «Квартет», «Лебедь, Щука и Рак», «Лисица и виноград», «Слон и Моська», «Стрекоза и Муравей», «Тришкин кафтан» и др. Какие черты характера людей и отношения между людьми смоделировал в них автор? Обсудите эти вопросы в группе.

4. Решите, составив математическую модель, следующую задачу.

Теплоход прошёл 4 км против течения реки, а затем прошёл ещё 33 км по течению, затратив на весь путь один час. Найдите собственную скорость теплохода, если скорость течения реки равна 6,5 км/ч.

5. Требуется спроектировать электрическую цепь, показывающую итог тайного голосования комиссии в составе трёх членов. При голосовании «за» член комиссии нажимает кнопку. Предложение считается принятым, если оно собирает большинство голосов. В этом случае загорается лампочка.

6. Решите, составив логическую модель, следующую задачу.

На международных соревнованиях по прыжкам в воду первые пять мест заняли спортсмены из Германии, Италии, Китая, России и Украины. Ещё до начала соревнований эксперты высказали свои предположения об их итогах:

1) Первое место займёт спортсмен из Китая, а спортсмен из Украины будет третьим.
2) Украина будет на последнем месте, а Германия — на предпоследнем.
3) Германия точно будет четвёртой, а первое место займёт Китай.
4) Россия будет первой, а Италия — на втором месте.
5) Италия будет пятой, а победит Германия.

По окончании соревнований выяснилось, что каждый эксперт был прав только в одном утверждении. Какие места в соревновании заняли участники?

7. В середине прошлого века экономисты оценили ежегодный объём вычислений, необходимых для эффективного управления народным хозяйством страны. Он составил 1017 операций. Можно ли справиться с таким объёмом вычислений за год, если привлечь к работе миллион вычислителей, каждый из которых способен выполнять одну операцию в секунду?

8. Приведите примеры использования компьютерных моделей. Найдите соответствующую информацию в сети Интернет.

9. В Единой коллекции цифровых образовательных ресурсов найдите лабораторную работу «Изучение закона сохранения импульса». В её основу положена математическая модель, описывающая движение тела, брошенного под углом к горизонту, с последующим делением тела на два осколка. Экспериментально проверьте закон сохранения импульса, выполнив работу согласно имеющемуся в ней описанию.

10. В Единой коллекции цифровых образовательных ресурсов найдите игру «Равноплечий рычаг». Изучите правила игры. Вспомните физическую закономерность, положенную в её основу. Попытайтесь «победить» компьютер и сформулировать выигрышную стратегию.

Электронное приложение к уроку

Cкачать материалы урока