Урок 5
§1.4 Табличные информационные модели

В табличных информационных моделях информация об объектах представляется в виде прямоугольной таблицы, состоящей из столбцов и строк.

Вам хорошо известно табличное представление расписания уроков, в табличной форме представляются расписания движения автобусов, самолётов, поездов и многое другое.

Представленная в таблице информация наглядна, компактна и легкообозрима.

1.4.1. Представление данных в табличной форме

В качестве информационных моделей объектов, обладающих одинаковыми наборами свойств, как правило, используются таблицы типа «объект—свойство».

Например, информацию о регионах нашей страны можно представить с помощью таблицы, фрагмент которой приведён в табл. 1.1.

В этой таблице каждая строка содержит информацию об одном объекте — регионе; столбцы — отдельные характеристики (свойства) рассматриваемых объектов: название, дата образования, площадь и т. д. Такие таблицы могут содержать числовую, текстовую и графическую информацию.

Таблица 1.1

Регионы Российской Федерации

---

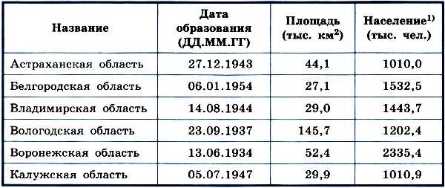
¹⁾ Численность населения приведена по результатам переписи населения России 2010 г.

Располагаете ли вы аналогичной информацией о своём регионе? Уточните информацию о современной численности населения вашего региона.

В таблицах типа «объект — объект» отражается взаимосвязь между объектами одного или нескольких классов. Например, в школьных журналах есть таблица «Сведения о количестве уроков, пропущенных обучающимися»; её фрагмент представлен в табл. 1.2.

Таблица 1.2

Сведения о пропусках уроков

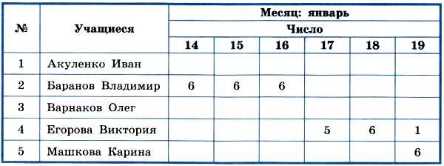
В этой таблице отражена связь «количество пропущенных уроков» между объектами класса «Учащиеся» и объектами класса «Число».

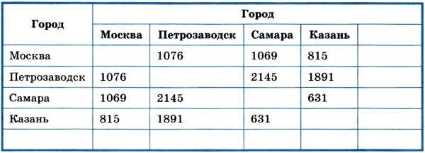
В таблице «Расстояния между городами» (табл. 1.3) представлены расстояния между парами объектов, принадлежащих одному классу «Город». Создайте эту таблицу в текстовом редакторе и добавьте в свободные строку и столбец информацию о своём населённом пункте.

Таблица 1.3

Расстояния между городами (км)

В форме таблицы «объект-объект» можно представить информацию о наличии границ (сухопутной, морской, озёрной, речной) России с другими странами; её фрагмент представлен в табл. 1.4.

Таблица 1.4

Граница Российской Федерации

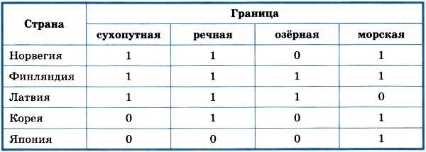
Если граница соответствующего вида есть, то в нужную ячейку ставится 1, а если нет — 0.

Важная особенность этой таблицы состоит в том, что в ней фиксируются не количественные («Сколько?»), а качественные свойства (наличие/отсутствие связи между объектами).

1.4.2. Использование таблиц при решении задач

Рассмотрим несколько примеров задач, которые удобно решать с помощью табличных информационных моделей.

Пример 1. Два игрока играют в следующую игру. Перед ними лежат две кучи камней, в первой из которых 3 камня, а во второй — 2 камня. У каждого игрока неограниченно много камней. Игроки ходят по очереди. Ход состоит в том, что игрок или увеличивает в 3 раза число камней в какой-то куче, или добавляет 1 камень в какую-то кучу. Выигрывает игрок, после хода которого общее число камней в двух кучах становится не менее 16. Кто выигрывает при безошибочной игре — игрок, делающий первый ход, или игрок, делающий второй ход? Каким должен быть первый ход выигрывающего игрока? Ответ обоснуйте. Ранее мы рассмотрели способ записи решения подобных задач с помощью дерева. Сейчас оформим решение в виде таблицы (табл. 1.5).

Таблица 1.5

Таблица игры

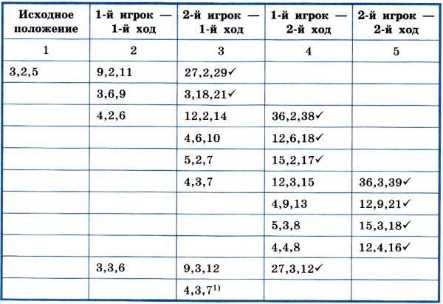
¹⁾ Вариант (как повторный) исключается из дальнейшего рассмотрения

.

Три числа в каждой ячейке таблицы обозначают соответственно количество камней в кучах и их сумму. В первом столбце зафиксировано распределение камней перед игрой (исходное положение).

Во втором столбце рассмотрены все возможные варианты ходов первого игрока; победить с первого хода он не может.

В третьем столбце рассмотрены имеющиеся выигрышные варианты ходов второго игрока (отмечены «галочкой»). При безошибочной игре первого игрока такие ситуации возникнуть не должны. Поэтому рассматриваем все возможные ходы второго игрока в случаях, когда у него нет выигрышного хода. Если получены одинаковые варианты, то все из них, кроме одного, исключаем из дальнейшего рассмотрения.

В четвёртом столбце отмечены имеющиеся выигрышные варианты второго хода первого игрока. При безошибочной игре второго игрока такие ситуации возникнуть не должны. Поэтому рассматриваем все возможные ходы первого игрока в случае, когда у него нет выигрышного хода.

В пятом столбце отмечены выигрышные ходы второго игрока, имеющиеся при всех вариантах хода первого игрока.

Таким образом, при безошибочной игре соперников побеждает второй игрок. Его первый ход должен быть таким, чтобы в кучах стало 4 и 3 камня.

Пример 2. С помощью взвешенного графа на рис. 1.6, в представлена схема дорог, соединяющих населённые пункты А, В, С, D, Е. Построим таблицу, соответствующую этому графу (рис. 1.12).

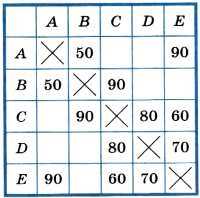
Рис. 1.12. Весовая матрица

Если между парой населённых пунктов существует дорога, то в ячейку на пересечении соответствующих строки и столбца записывается число, равное её длине. Имеющиеся в таблице пустые клетки означают, что дорог между соответствующими населёнными пунктами нет. Построенная таким образом таблица называется весовой матрицей.

Для решения некоторых задач бывает удобно по имеющейся таблице строить граф. При этом одной и той же таблице могут соответствовать графы, внешне не похожие друг на друга. Например, рассмотренной выше таблице кроме графа на рис. 1.6, в соответствует граф на рис. 1.13.

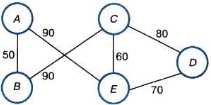
Рис. 1.13. Вариант графа, представляющего схему дорог

Пример 3. Таблицы типа «объект—объект» удобно использовать для решения логических задач, в которых требуется установить взаимно однозначное соответствие между объектами нескольких классов. Рассмотрим задачу, в которой объекты связаны тремя парами отношений.

Три подружки — Аня, Света и Настя — купили различные молочные коктейли в белом, голубом и зелёном стаканчиках. Ане достался не белый стаканчик, а Свете — не голубой. В белом стаканчике не банановый коктейль. В голубой стаканчик налит ванильный коктейль. Света не любит клубничный коктейль.

Требуется выяснить, какой коктейль и в каком стаканчике купила каждая из девочек.

Создадим три следующие таблицы:

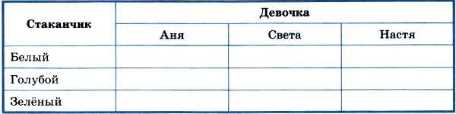
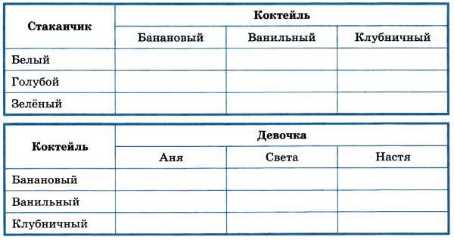
Отметим в таблицах информацию, содержащуюся в условии задачи:

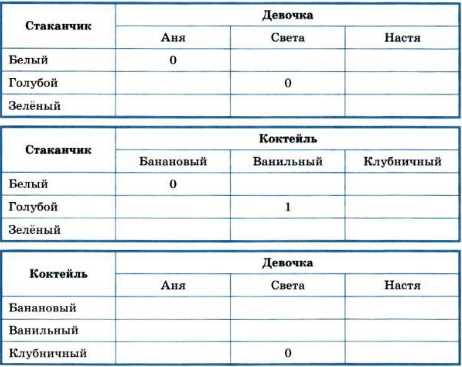
Имеющейся во второй таблице информации достаточно для того, чтобы заполнить всю эту таблицу:

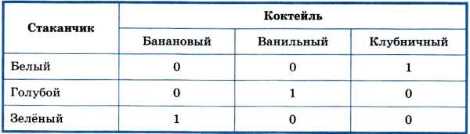
Используя факты, что Света купила не клубничный коктейль и что этот коктейль был налит в белый стаканчик, заполняем всю первую таблицу:

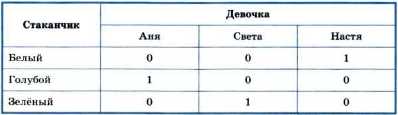
На основании информации в первой и второй таблицах можем заполнить всю третью таблицу:

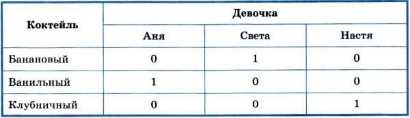
Ответ: Аня купила ванильный коктейль в голубом стаканчике, Света — банановый коктейль в зелёном стаканчике, Настя — клубничный коктейль в белом стаканчике.

САМОЕ ГЛАВНОЕ

В табличных информационных моделях информация об объекте представляется в виде прямоугольной таблицы, состоящей из столбцов и строк. Представленная в таблице информация наглядна, компактна и легкообозрима.

Таблица типа «объект—свойство» — это таблица, содержащая информацию о свойствах отдельных объектов, принадлежащих одному классу.

Таблица типа «объект—объект» — это таблица, содержащая информацию о некотором одном свойстве пар объектов, чаще всего принадлежащих разным классам.

Вопросы и задания

1. Ознакомьтесь с материалами презентации к параграфу, содержащейся в электронном приложении к учебнику. Что вы можете сказать о формах представления информации в презентации и в учебнике? Какими слайдами вы могли бы дополнить презентацию?

2. Какие преимущества обеспечивают табличные информационные модели по сравнению со словесными описаниями? Приведите пример.

3. Приведите примеры табличных информационных моделей, с которыми вы имеете дело:

а) на уроках в школе;
б) в повседневной жизни.

4. К какому типу относится таблица «Табель успеваемости», расположенная в конце вашего дневника?

5. Узнайте, в каких случаях в ячейку таблицы ставится знак х. Почему мы использовали этот знак в таблице (пример 2)?

6. Два игрока играют в следующую игру. Перед ними лежат две кучи камней, в первой из которых 1 камень, а во второй — 2 камня. У каждого игрока неограниченно много камней. Игроки ходят по очереди. Ход состоит в том, что игрок или увеличивает в 3 раза число камней в какой-то куче, или добавляет 2 камня в какую-то кучу. Выигрывает игрок, после хода которого общее число камней в двух кучах становится не менее 17. Кто выигрывает при безошибочной игре обоих игроков — игрок, делающий первый ход, или игрок, делающий второй ход? Каким должен быть первый ход выигрывающего игрока? Ответ обоснуйте.

7. Таблица стоимости перевозок устроена следующим образом: числа, стоящие на пересечениях строк и столбцов таблиц, означают стоимость перевозок между соответствующими соседними станциями. Если пересечение строки и столбца пусто, то станции не являются соседними. Стоимость перевозок по маршруту складывается из стоимостей перевозок между соседними станциями. Перевозки между населёнными пунктами А, В, С, В, Е осуществляют три компании, представившие стоимость своих услуг в табличной форме. Какая компания обеспечивает минимальную стоимость перевозок из А в В?

8. Соревнования по плаванию были в самом разгаре, когда стало ясно, что первые четыре места займут мальчики из пятёрки лидеров. Их имена: Валерий, Николай, Михаил, Игорь, Эдуард, фамилии: Симаков, Чигрин, Зимин, Копылов, Блинов (имена и фамилии названы в произвольном порядке). Нашлись знатоки, которые предсказали, что первое место займёт Копылов, второе — Валерий, третье — Чигрин, четвёртое — Эдуард. Но ни один из ребят не занял того места, какое ему предсказывали. На самом деле первое место завоевал Михаил, второе — Симаков, третье — Николай, четвёртое — Блинов, а Чигрин не попал в четвёрку сильнейших. Назовите имя и фамилию каждого из лидеров.

9. В Норильске, Москве, Ростове и Пятигорске живут четыре супружеские пары (в каждом городе — одна пара). Имена этих супругов: Антон, Борис, Давид, Григорий, Ольга, Мария, Светлана, Екатерина. Антон живёт в Норильске, Борис и Ольга — супруги, Григорий и Светлана не живут в одном городе, Мария живёт в Москве, Светлана — в Ростове. В каком городе живёт каждая из супружеских пар?

10. Постройте граф, отражающий разновидности информационных моделей.

Электронное приложение к уроку

Cкачать материалы урока