Ключевые слова:
• подпрограмма
• процедура
• функция
• рекурсивная функция
Урок 16
§2.4 Запись вспомогательных алгоритмов на языке Паскаль
Запись вспомогательных алгоритмов в языках программирования осуществляется с помощью подпрограмм. В Паскале подпрограмма является частью основной программы. Её описание располагается между разделом var и программным блоком главной программы. Если подпрограмм несколько, то их описания располагаются в произвольном порядке одно за другим.
Структура описания подпрограммы аналогична структуре главной программы. Описание подпрограммы начинается с заголовка и заканчивается оператором end.
В Паскале различают два вида подпрограмм: процедуры и функции.
2.4.1. Процедуры
 Процедура — подпрограмма, имеющая произвольное количество входных и выходных данных.
Процедура — подпрограмма, имеющая произвольное количество входных и выходных данных.
Описание процедуры имеет вид:

В заголовке процедуры после её имени приводится перечень формальных параметров и их типов. Входные параметры, значения которых не изменяются в программе, должны быть параметрами-значениями. Выходные (результирующие) параметры должны быть параметрами-переменными.
Для вызова процедуры достаточно указать её имя со списком фактических параметров. В качестве параметров-значений можно указывать имена переменных, константы и выражения.
Например, заголовок процедуры вычисления наибольшего общего делителя может быть описан так:
procedure nod (a, b: integer; var с: integer);
Возможны следующие варианты вызова этой процедуры:
nod (36, 15, z) — в качестве параметров-значений использованы константы;
nod (х, у, z) — в качестве параметров-значений использованы имена переменных;
nod (х+у, 15, z) — в качестве параметров-значений использованы выражение и константа.
В любом случае между фактическими и формальными параметрами должно быть полное соответствие по количеству, порядку следования и типу.
Пример 1. Напишем процедуру для нахождения наибольшего общего делителя двух чисел с помощью алгоритма Евклида. Используем её для нахождения наибольшего общего делителя следующих шести чисел: 16, 32, 40, 64, 80 и 128.

Измените программу так, чтобы с её помощью можно было найти:
а) наибольший общий делитель следующих пяти чисел: 12, 24, 30, 48 и 51;
б) наибольший общий делитель произвольных десяти целых двузначных чисел.
2.4.2. Функции
Описание функции имеет вид:

В заголовке функции после её имени приводится описание входных данных — указывается перечень формальных параметров и их типов. Там же указывается тип самой функции, т. е. тип результата.
 Функция — подпрограмма, имеющая единственный результат, записываемый в ячейку памяти, имя которой совпадает с именем функции. Поэтому в блоке функции обязательно должен присутствовать оператор <имя_функции>: =<результат>.
Функция — подпрограмма, имеющая единственный результат, записываемый в ячейку памяти, имя которой совпадает с именем функции. Поэтому в блоке функции обязательно должен присутствовать оператор <имя_функции>: =<результат>.
Для вызова функции достаточно указать её имя со списком фактических параметров в любом выражении, в условиях (после слов if, while, until) или в операторе write главной программы.
Пример 2. Напишем программу нахождения максимального из четырёх целых чисел, использующую функцию поиска максимального из двух чисел:

Измените программу так, чтобы с её помощью можно было найти:
а) максимальное из чисел а, b, с;
б) максимальное из чисел b, с, d;
в) минимальное из четырёх чисел;
г) разность максимального и минимального из четырёх чисел.
Пример 3. В январе Саше подарили пару новорождённых кроликов. Через два месяца они дали первый приплод — новую пару кроликов, а затем давали приплод по паре кроликов каждый месяц. Каждая новая пара также даёт первый приплод (пару кроликов) через два месяца, а затем — по паре кроликов каждый месяц. Сколько пар кроликов будет у Саши в декабре?
Составим математическую модель этой задачи. Обозначим через f(n) количество пар кроликов в месяце с номером n. По условию задачи, f(1) = 1, f(2) = 1, f(3) = 2. Из двух пар, имеющихся в марте, дать приплод в апреле сможет только одна: f(4) = 3. Из пар, имеющихся в апреле, дать приплод в мае смогут только пары, родившиеся в марте и ранее: f(5) = f(4) + f(3) = 3 + 2 = 5. В общем случае: f(n) = f(n - 1) + f(n - 2), n ≥ 3.
Числа 1, 1, 2, 3, 5, 8,... образуют так называемую последовательность Фибоначчи, названную в честь итальянского математика, впервые решившего соответствующую задачу ещё в начале XIII века.
Оформим в виде функции вычисление члена последовательности Фибоначчи.

Полученная функция — рекурсивная; в ней реализован способ вычисления очередного значения функции через вычисление её предшествующих значений.
Напишите программу, вычисляющую и выводящую 10 первых членов последовательности Фибоначи.
САМОЕ ГЛАВНОЕ
Запись вспомогательных алгоритмов в языках программирования осуществляется с помощью подпрограмм. В Паскале различают два вида подпрограмм: процедуры и функции.
Процедура — подпрограмма, имеющая произвольное количество входных и выходных данных.
Функция — подпрограмма, имеющая единственный результат, записываемый в ячейку памяти, имя которой совпадает с именем функции.
Вопросы и задания
1. Ознакомьтесь с материалами презентации к параграфу, содержащейся в электронном приложении к учебнику. Дополняет ли презентация информацию, содержащуюся в тексте параграфа?
2. Для чего используются подпрограммы?
3. В чём основное различие процедур и функций?
4. Напишите программу вычисления наименьшего общего кратного следующих четырёх чисел: 36, 54, 18 и 15. Используйте процедуру вычисления наибольшего общего делителя двух чисел.
5. Напишите программу перестановки значений переменных а, b, с в порядке возрастания, т. е. так, чтобы а < b < с. Используйте процедуру swap.

Исходные данные вводятся с клавиатуры.
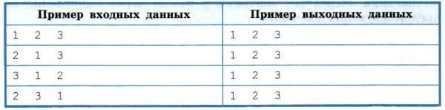
6. Видоизмените программу сортировки массива выбором так, чтобы в ней использовалась процедура выбора наибольшего элемента массива.
7. Напишите программу вычисления выражения: s = 1! + 2! + 3! +...+ n!
Здесь n! — факториал числа n. n! = 1*2*...*(n—1)*n. Используйте функцию вычисления факториала.
Факториал — функция, определённая на множестве неотрицательных целых чисел. Название происходит от лат. factorialis — действующий, производящий, умножающий;
обозначается n!, произносится эн факториал. Факториал натурального числа n определяется как произведение всех натуральных чисел от 1 до n включительно:
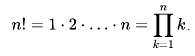
Например,
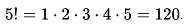
Из определения факториала следует соотношение 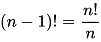 , откуда при n = 1 формально находим 0!=1.
, откуда при n = 1 формально находим 0!=1.
8. Напишите программу вычисления выражения:
s = х3 + х5 + хn, где х и n вводятся с клавиатуры. Используйте подпрограмму вычисления степени.
9. Напишите функцию, вычисляющую длину отрезка по координатам его концов. Напишите программу, вычисляющую периметр треугольника по координатам его вершин с помощью этой функции.
10. Напишите функцию, вычисляющую площадь треугольника по целочисленным координатам его вершин. Напишите программу вычисления площади четырёхугольника по координатам его вершин с помощью этой функции.
 Тест "Запись вспомогательных алгоритмов"
Тест "Запись вспомогательных алгоритмов"




