Уроки 19 - 20
§3.2 Организация вычислений в электронных таблицах
Относительные, абсолютные и смешанные ссылки
Встроенные функции. Логические функции

Основным назначением электронных таблиц является организация всевозможных вычислений. Вы уже знаете, что:

• вычисление — это процесс расчёта по формулам;
• формула начинается со знака равенства и может включать в себя знаки операций, числа, ссылки и встроенные функции.

3.2.1. Относительные, абсолютные и смешанные ссылки

Ссылка указывает на ячейку или диапазон ячеек, содержащих данные, которые требуется использовать в формуле. Ссылки позволяют:

• использовать в одной формуле данные, находящиеся в разных частях электронной таблицы;
• использовать в нескольких формулах значение одной ячейки.

Различают два основных типа ссылок:

1) относительные — зависящие от положения формулы;
2) абсолютные — не зависящие от положения формулы.

Различие между относительными и абсолютными ссылками проявляется при копировании формулы из текущей ячейки в другие ячейки.

Относительные ссылки. Присутствующая в формуле относительная ссылка определяет расположение ячейки с данными относительно ячейки, в которой записана формула. При изменении позиции ячейки, содержащей формулу, изменяется и ссылка.

Рассмотрим формулу =А1ˆ2, записанную в ячейке А2. Она содержит относительную ссылку А1, которая воспринимается табличным процессором следующим образом: содержимое ячейки, находящееся на одну строку выше той, в которой находится формула, следует возвести в квадрат.

При копировании формулы вдоль столбца и вдоль строки относительная ссылка автоматически корректируется так:

• смещение на один столбец приводит к изменению в ссылке одной буквы в имени столбца;
• смещение на одну строку приводит к изменению в ссылке номера строки на единицу.

Например, при копировании формулы из ячейки А2 в ячейки В2, С2 и D2 относительная ссылка автоматически изменяется и рассмотренная выше формула приобретает вид: =В1ˆ2, =С1ˆ2, =D1ˆ2. При копировании этой же формулы в ячейки АЗ и А4 получим, соответственно, =А2ˆ2, =А3ˆ2 (рис. 3.4).

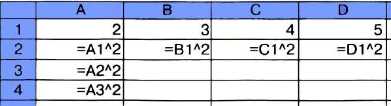
Рис. 3.4. Скопированная формула с относительной ссылкой

Пример 1. В 8 классе мы рассматривали задачу о численности населения некоторого города, ежегодно увеличивающейся на 5%. Проведём в электронных таблицах расчёт предполагаемой численности населения города в ближайшие 5 лет, если в текущем году она составляет 40 ООО человек.

Внесём в таблицу исходные данные, в ячейку ВЗ введём формулу =В2+0,05*В2 с относительными ссылками; скопируем формулу из ячейки ВЗ в диапазон ячеек В4:В7 (рис. 3.5).

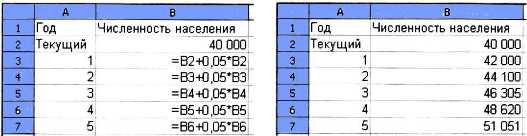
Рис. 3.5. Вид таблицы расчёта численности населения в режиме отображения формул и режиме отображения значений

Ежегодный расчёт численности населения мы (согласно условию задачи) осуществляли по одной и той же формуле, исходные данные для которой всегда находились в ячейке, расположенной в том же столбце, но на одну строку выше, чем расчётная формула. При копировании формулы, содержащей относительные ссылки, нужные нам изменения осуществлялись автоматически.

Абсолютные ссылки. Абсолютная ссылка в формуле всегда ссылается на ячейку, расположенную в определённом (фиксированном) месте. В абсолютной ссылке перед каждой буквой и цифрой помещается знак $, например $А$1. При изменении позиции ячейки, содержащей формулу, абсолютная ссылка не изменяется. При копировании формулы вдоль строк и вдоль столбцов абсолютная ссылка не корректируется (рис. 3.6).

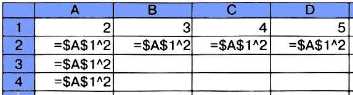
Рис. 3.6. Скопированная формула с абсолютной ссылкой

Пример 2. Некий гражданин открывает в банке счёт на сумму 10 ООО рублей. Ему сообщили, что каждый месяц сумма вклада будет увеличиваться на 1,2%. Для того чтобы узнать возможную сумму и приращение суммы вклада через 1, 2,..., 6 месяцев, гражданин провёл следующие расчёты (рис. 3.7).

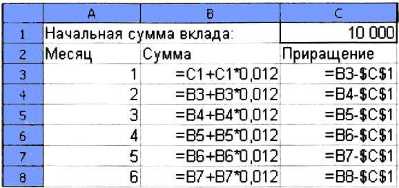
Рис. 3.7. Расчёт приращения суммы вклада

Прокомментируйте формулы в таблице на рис. 3.7.

Выполните аналогичные расчёты для начального вклада, равного 15 ООО рублям.

Смешанные ссылки. Смешанная ссылка содержит либо абсолютно адресуемый столбец и относительно адресуемую строку ($А1), либо относительно адресуемый столбец и абсолютно адресуемую строку (А$1). При изменении позиции ячейки, содержащей формулу, относительная часть адреса изменяется, а абсолютная часть адреса не изменяется.

При копировании или заполнении формулы вдоль строк и вдоль столбцов относительная часть ссылки автоматически корректируется, а абсолютная часть ссылки не корректируется (рис. 3.8).

Рис. 3.8. Скопированная формула со смешанной ссылкой

Чтобы преобразовать ссылку из относительной в абсолютную и наоборот, можно выделить её в строке ввода и нажать клавишу F4 (Microsoft Office Excel) или комбинацию клавиш Shift+F4 (OpenOffice Calc). Если выделить относительную ссылку, такую как А1, то при первом нажатии этой клавиши (комбинации клавиш) и для строки, и для столбца установятся абсолютные ссылки ($А$1). При втором нажатии абсолютную ссылку получит только строка (А$1). При третьем нажатии абсолютную ссылку получит только столбец ($А1). Если нажать клавишу F4 (комбинацию клавиш Shift+F4) ещё раз, то для столбца и строки снова установятся относительные ссылки (А1).

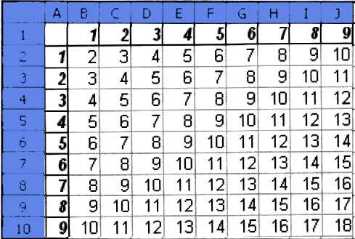
Пример 3. Требуется составить таблицу сложения чисел первого десятка, т. е. заполнить таблицу следующего вида:

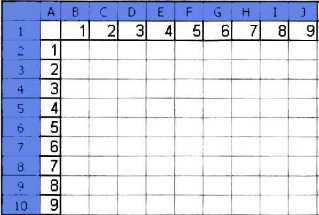
При заполнении любой ячейки этой таблицы складываются соответствующие ей значения ячеек столбца А и строки 1. Иначе говоря, у первого слагаемого неизменным остаётся имя столбца (на него следует дать абсолютную ссылку), но изменяется номер строки (на неё следует дать относительную ссылку); у второго слагаемого изменяется номер столбца (относительная ссылка), но остаётся неизменным номер строки (абсолютная ссылка).

Внесите в ячейку В2 формулу =$А2+В$1 и скопируйте её на весь диапазон B2:J10. У вас должна получиться таблица сложения, знакомая каждому первокласснику.

3.2.2. Встроенные функции

При обработке данных в электронных таблицах можно использовать встроенные функции — заранее определённые формулы. Функция возвращает результат выполнения действий над значениями, выступающими в качестве аргументов. Использование функций позволяет упростить формулы и сделать процесс вычислений более понятным.

В электронных таблицах реализовано несколько сотен встроенных функций, подразделяющихся на: математические, статистические, логические, текстовые, финансовые и др.

Каждая функция имеет уникальное имя, которое используется для её вызова. Имя, как правило, представляет собой сокращённое название функции на естественном языке. При выполнении табличных расчётов достаточно часто используются функции:

СУММ (SUM) — суммирование аргументов;

МИН (MIN) — определение наименьшего значения из списка аргументов;

МАКС (МАХ) — определение наибольшего значения из списка аргументов.

Диалоговое окно Мастер функций позволяет упростить создание формул и свести к минимуму количество опечаток и синтаксических ошибок. При вводе функции в формулу диалоговое окно Мастер функций отображает имя функции, все её аргументы, описание функции и каждого из аргументов, текущий результат функции и всей формулы.

Пример 4. Правила судейства в международных соревнованиях по одному из видов спорта таковы:

1) выступление каждого спортсмена оценивают N судей;
2) максимальная и минимальная оценки (по одной, если их несколько) каждого спортсмена отбрасываются;
3) в зачёт спортсмену идёт среднее арифметическое оставшихся оценок.

Информация о соревнованиях представлена в электронной таблице:

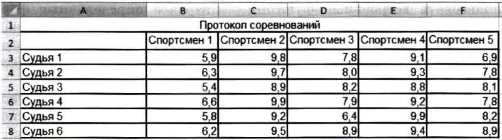
Требуется подсчитать оценки всех участников соревнований и определить оценку победителя. Для этого:

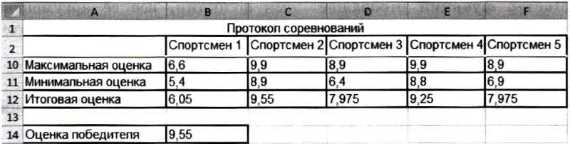
1) в ячейки А10, All, А12 и А14 заносим тексты «Максимальная оценка», «Минимальная оценка», «Итоговая оценка», «Оценка победителя»;
2) в ячейку В10 заносим формулу =МАКС(ВЗ:В8); копируем содержимое ячейки В10 в ячейки C10:F10;
3) в ячейку В11 заносим формулу =МИН(ВЗ:В8); копируем содержимое ячейки В10 в ячейки C11:F11;
4) в ячейку В12 заносим формулу =(СУММ(ВЗ:В8)-В10-В11)/4; копируем содержимое ячейки В12 в ячейки C12:F12;
5) в ячейку В14 заносим формулу =MAKC(B12:F12).

Результат решения задачи:

3.2.3. Логические функции

При изучении предшествующего материала вы неоднократно встречались с логическими операциями НЕ, И, ИЛИ (not, and, or). Построенные с их помощью логические выражения вы использовали при организации поиска в базах данных, при программировании различных вычислительных процессов.

Реализованы логические операции и в электронных таблицах, но здесь они представлены как функции: сначала записывается имя логической операции, а затем в круглых скобках перечисляются логические операнды.

Например, логическое выражение, соответствующее двойному неравенству 0<А1<10, в электронных таблицах будет записано как И(А1>0;А1<10) (AND(A1>0;A1<10)).

Вспомните, как аналогичное логическое выражение мы записывали при знакомстве с базами данных и языком программирования Паскаль.

Пример 5. Вычислим в электронных таблицах значения логического выражения НЕ А И НЕ В при всех возможных значениях входящих в него логических переменных.

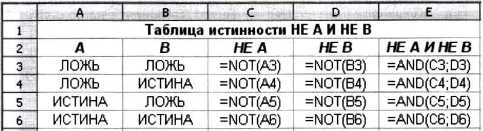
При решении этой задачи мы следовали известному вам алгоритму построения таблицы истинности для логического выражения. Вычисления в диапазонах ячеек С3:С6, D3:D6, Е3:Е6 проводятся компьютером по заданным нами формулам.

Для проверки условий при выполнении расчётов в электронных таблицах реализована логическая функция ЕСЛИ (IF), называемая условной функцией.

Условная функция имеет следующую структуру:

ЕСЛИ (<условие>; <действие1>; <действие2)

Здесь <условие> — логическое выражение, т. е. любое выражение, построенное с помощью операций отношения и логических операций, принимающее значение ИСТИНА или ЛОЖЬ.

Если логическое выражение истинно, то значение ячейки, в которую записана условная функция, определяет <действие1>, если ложно — <действие2>¹⁾.

---

¹⁾ Действием может быть вычисление формулы, ввод числа или текста в ячейку.

Что вам напоминает структура условной функции?

Пример 6. Рассмотрим задачу о приёме в школьную баскетбольную команду: ученик может быть принят в эту команду, если его рост не менее 170 см.

Данные о претендентах (фамилия, рост) представлены в электронной таблице.

Использование условной функции в диапазоне ячеек С3:С8 позволяет вынести решение (принят/не принят) по каждому претенденту.

Функция СЧЁТЕСЛИ (COUNTIF) позволяет подсчитать количество ячеек в диапазоне, удовлетворяющих заданному условию. С помощью этой функции в ячейке С9 подсчитывается число претендентов, прошедших отбор в команду.

Функция СУММЕСЛИ (SUMMIF) суммирует значения диапазона, удовлетворяющие заданному условию.

В Единой коллекции цифровых образовательных ресурсов размещён «Интерактивный задачник. Раздел "Логические формулы в электронных таблицах"» (119424). Попытайтесь самостоятельно выполнить имеющиеся в нём задания в режимах «Тренировка» и «Зачёт».

САМОЕ ГЛАВНОЕ

Для организации вычислений в электронных таблицах используются формулы, которые могут включать в себя ссылки и функции.

Различают относительные, абсолютные и смешанные ссылки.

Относительная ссылка определяет расположение ячейки с данными относительно ячейки, в которой записана формула. При изменении позиции ячейки, содержащей формулу, изменяется и ссылка.

Абсолютная ссылка всегда ссылается на ячейку, расположенную в определённом месте. При изменении позиции ячейки, содержащей формулу, абсолютная ссылка не изменяется.

Смешанная ссылка содержит либо абсолютно адресуемый столбец и относительно адресуемую строку, либо относительно адресуемый столбец и абсолютно адресуемую строку. При изменении позиции ячейки, содержащей формулу, относительная часть адреса изменяется, а абсолютная часть адреса не изменяется.

Функции — это заранее определённые и встроенные в электронные таблицы формулы. Использование функций позволяет упростить формулы и сделать процесс вычислений более понятным.

Вопросы и задания

1. Ознакомьтесь с материалами презентации к параграфу, содержащейся в электронном приложении к учебнику. Используйте эти материалы при подготовке ответов на вопросы и выполнении заданий.

2. Назовите основные типы ссылок.

3. Охарактеризуйте относительный тип ссылок.

4. По данным электронной таблицы определите значение в ячейке С1.

5. Дан фрагмент электронной таблицы:

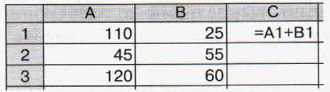
Определите значения в ячейках С2 и СЗ после копирования в них формулы из ячейки С1. Проверьте свои предположения на компьютере.

6. Дан фрагмент электронной таблицы:

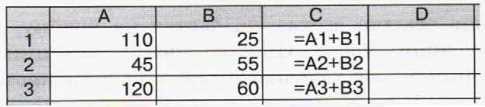
Определите значения в ячейках диапазона D1:D3 после копирования в них формулы из ячейки СЗ. Проверьте свои предположения на компьютере.

7. Охарактеризуйте абсолютный тип ссылок.

8. Дан фрагмент электронной таблицы:

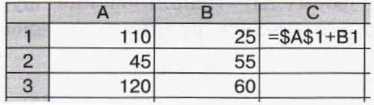
Определите значения в ячейках С2 и СЗ после копирования в них формулы из ячейки С1. Проверьте свои предположения на компьютере.

9. Охарактеризуйте смешанный тип ссылок.

10. Дан фрагмент электронной таблицы:

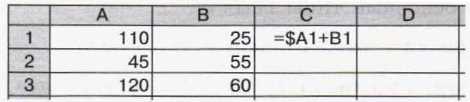
Определите значения в ячейках диапазона C1:D3 после копирования в них формулы из ячейки С1. Проверьте свои предположения на компьютере.

11. Как можно изменить тип ссылки?

12. О чём идёт речь в следующем высказывании: «Знак доллара "замораживает" как весь адрес, так и его отдельную часть»? Дайте развёрнутый комментарий к высказыванию, основываясь на материале параграфа. Обсудите этот вопрос в группе.

13. Для чего нужны встроенные функции?

14. Какие категории встроенных функций реализованы в табличном процессоре, имеющемся в вашем распоряжении?

15. Дан фрагмент электронной таблицы:

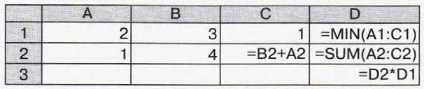
Определите значение в ячейке D3.

16. Какая из формул не содержит ошибок?

а) =ЕСЛИ ((С4>4) И (С5>4));"Принят!";"Не принят")
б) =ЕСЛИ (M(D2=0;B2/4);D3-A1;D3+A1)
в) =ЕСЛИ ((А4=0 И D1<0);1;0)
г) =ЕСЛИ (ИЛИ(А2>10;С2>10);1;"ура!")

17. В ячейке А5 электронной таблицы находится суммарная стоимость товаров, заказанных Иваном А. в интернет-магазине. Формула, позволяющая подсчитать полную стоимость заказа, с учётом стоимости его доставки, имеет вид:

=ЕСЛИ(А5>=2000;А5;А5+150).

По данной формуле постройте блок-схему. Определите, какие льготы предоставляются покупателю в случае, если суммарная стоимость заказанных им товаров превышает 2000.

18. Оплата за аренду конференц-зала вычисляется по следующим правилам: каждый из первых четырёх часов аренды стоит 1000 рублей, каждый последующий час — 750 рублей. В ячейке В8 электронной таблицы находится количество полных часов аренды зала. Какая из формул позволяет подсчитать полную стоимость аренды зала?

а) =ЕСЛИ(В8<=4;В8*1000;4000+В8*750)
б) =ЕСЛИ(В8<=4;В8*1000;В8*1000+(В8-4)*750)
в) =ЕСЛИ(В8<=4;В8*1000;(В8+(В8-4)*750)
г) =ЕСЛИ(В8<=4;В8*1000;4000 +(В8-4)*750)

Электронное приложение к уроку

Cкачать материалы урока