Уроки 4 - 7
Графический учебный исполнитель
(§ 4. Графический учебный исполнитель)
Работа с учебным исполнителем алгоритмов: построение линейных алгоритмов
Содержание урока
Назначение и возможности графического исполнителя (ГРИС)
Линейные программы для ГРИС
Компьютерный практикум ЦОР. Графический учебный исполнитель
Линейные программы для ГРИС
Будем осваивать программирование на примерах решения конкретных задач. С новыми командами СКИ будем знакомиться по мере появления потребности в них.
Задача 1. Составим и выполним программу, по которой ГРИС нарисует на поле букву «Т». Пусть длина вертикального и горизонтального отрезков должна быть равна четырем шагам.
Исходное состояние — чистый лист. Исполнитель находится в точке, где будет находиться левый конец горизонтального отрезка, направление — на восток.
Результат выполнения программы показан ниже.
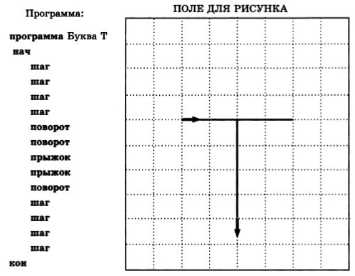
Структура такой программы (алгоритма) называется линейной. Команды выполняются одна за другой, каждая только один раз.
Для решения этой задачи оказалось достаточно той части СКИ, которая используется в режиме прямого управления.
Коротко о главном:
- ГРИС — это графический исполнитель, назначение которого — получение чертежей, рисунков на экране дисплея.
- Управление ГРИС может происходить в режиме прямого управления или в режиме программного управления.
- С помощью команд шаг, поворот, прыжок в пределах рабочего поля можно построить любой рисунок, состоящий из вертикальных и горизонтальных отрезков. Структура управляющего алгоритма при этом будет линейной.
Вопросы и задания:
- Какую работу может выполнять ГРИС?
- Что представляет собой среда исполнителя ГРИС?
- В чем разница между управлением в прямом режиме и в программном режиме?
- Какие простые команды входят в СКИ ГРИС; как они выполняются?
- В какой последовательности происходит выполнение команд в линейном алгоритме?
- Может ли данный исполнитель нарисовать: прямоугольник, треугольник, пятиконечную звезду, буквы «Н», «Х», «Р», «М»?
- Составьте программы рисования символов «Е», «П», «Б», «Ч», «Ц», «Ш», а также других фигур, состоящих из горизонтальных и вертикальных отрезков.


