Уроки 16 - 19
Ветвления
Использование двухшаговой детализации
(§ 7. Ветвление и последовательная детализация алгоритма)
Использование метода последовательной детализации для построения алгоритма
Использование ветвлений
Содержание урока
Пример задачи с двухшаговой детализацией
Дополнительный материал к главе I (§§ 1 - 7). Автоматизированные и автоматические системы управления
Дополнительный материал к главе I (§§ 1 - 7). Использование рекурсивных процедур
Компьютерный практикум ЦОР. Ветвление и последовательная детализация алгоритма
Компьютерный практикум ЦОР. Ветвление. Использование двухшаговой детализации
Дополнительный материал к главе I (§§ 1 - 7)
1.2. Использование рекурсивных процедур
Вернемся к вопросу об использовании процедур при составлении программ управления исполнителями алгоритмов (см. § 5 нашего учебника). Но это будет особый вид процедур, которые называются рекурсивными процедурами.
 Рекурсивной называется процедура, в которой имеется обращение к самой себе.
Рекурсивной называется процедура, в которой имеется обращение к самой себе.
Не все учебные исполнители алгоритмов допускают использование рекурсивных процедур (рекурсии). Такая возможность имеется в учебной программе «Стрелочка», реализующей один из вариантов графического исполнителя алгоритмов (ГРИС). При программировании некоторых задач рекурсия может служить альтернативой циклу.
Приведем пример использования в программе для ГРИС «Стрелочка» рекурсивной процедуры вместо цикла.
Пусть начальное положения «Стрелочки» — произвольная точка в первой строке рабочего поля, направление «вправо» (рис. 1.16). Требуется построить линию, идущую из этой точки до правой границы области.
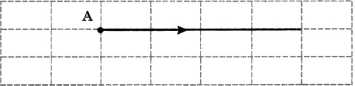
Рис. 1.16
Сначала приведем на языке «Стрелочки» программу, в которой используется цикл.
алгоритм ПУТЬ_1_0
Дано: исполнитель в точке А
Надо: воспроизвести образец
нач
пока впереди НЕ стена
нц
шаг
кц
кон
А теперь воспользуемся рекурсией, для чего опишем процедуру ЛИНИЯ_1.
алгоритм ПУТЬ_1_1
Дано: Исполнитель в точке А
Надо: Воспроизвести образец
нач
делай ЛИНИЯ_1
кон
процедура ЛИНИЯ_1
шаг
делай ЛИНИЯ_1
конец процедуры
В теле этой процедуры присутствует команда обращения к самой себе: делай ЛИНИЯ_1.
Пошаговое исполнение (трассировка) такой программы иллюстрируется следующей трассировочной таблицей в случае, если «Стрелочка» вначале располагается за два шага до стенки.
Трассировка алгоритма

В этом случае завершение исполнения алгоритма произойдет аварийным образом (ситуация НЕ МОГУ).
Дело в том, что в данном алгоритме мы имеем дело с бесконечно повторяющимся рекурсивным обращением к процедуре, что недопустимо. Количество обращений процедуры к самой себе при ее исполнении называется глубиной рекурсии. Глубина рекурсии должна быть конечной. Для исполнителя «Стрелочка» естественным ограничением количества обращений процедуры самой к себе может служить только достижение стены. Следовательно, рекурсивный вызов в процедуре надо поместить в команду ветвления, проверяющую условие достижения стены. Вот новый вариант алгоритма.
алгоритм ПУТЬ_1_2
Дано: Исполнитель в точке А
Надо: Воспроизвести образец
нач
делай ЛИНИЯ 2
кон
процедура ЛИНИЯ 2
если впереди НЕ стена
то
шаг
делай ЛИНИЯ 2
все
конец процедуры
Трассировка этого алгоритма представлена в следующей таблице:
Трассировка алгоритма

Поскольку в описании алгоритма присутствует «точка остановки» (условие окончания исполнения алгоритма), исполнитель «Стрелочка», дойдя до стены, остановится.
Возникает вопрос: а стоит ли пользоваться рекурсией, если задача решается с помощью цикла? Немного усложним исходную задачу: требуется построить линию, идущую из данной точки, до правой границы области, после чего исполнитель должен вернуться в исходную точку А.
При использовании рекурсии решение этой задачи запишется достаточно просто, в то время как циклический алгоритм для такой задачи построить невозможно.
алгоритм ПУТЬ_2
Дано: Исполнитель в точке А
Надо: Воспроизвести образец
нач
делай ЛИНИЯ_3
кон
процедура ЛИНИЯ З
если впереди НЕ стена
то
шаг
делай ЛИНИЯ_3
прыжок
иначе
поворот
поворот
все
конец процедуры
Трассировка алгоритма ПУТЬ_2 для исходного положения исполнителя за два шага до стенки показана в следующей таблице.
Трассировка алгоритма
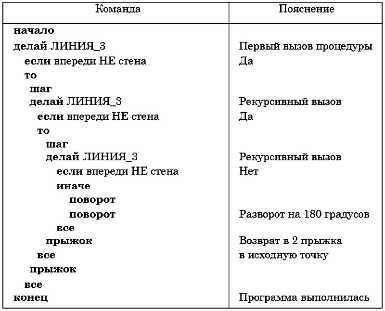
Если при выполнении процедуры происходит рекурсивное обращение к ней самой, то это значит, что не произошел выход из этой процедуры при предыдущем обращении. Этот выход откладывается на будущее. Затем, после окончания рекурсивных обращений, все отложенные выходы отрабатываются в порядке, обратном порядку рекурсивных обращений. В приведенной программе отработка отложенных выходов начинается с выполнения команды поворот.
Таким образом, существуют задачи, для которых использование рекурсии позволяет получить достаточно компактную запись алгоритма, в то время как его «циклическая версия» может оказаться либо очень сложной, либо вообще не реализуемой.
Коротко о главном
Рекурсивной называется процедура, в которой имеется обращение к самой себе.
Использование рекурсии может быть эквивалентом использованию цикла.
Существуют задачи, для которых рекурсивное решение является наиболее оптимальным или единственно возможным.
Вопросы и задания
1. Что такое рекурсивная процедура?
2. В каком порядке происходит выход из последовательности рекурсивных обращений?
3. Попробуйте разобраться, какую задачу решает следующая программа, содержащая рекурсивную процедуру. Реализуйте ее в среде исполнителя «Стрелочка».
алгоритм ФИГУРА-1
Дано: Исполнитель в точке А
Надо: Воспроизвести образец
нач
делай ЛИНИЯ
поворот
поворот
поворот
шаг
шаг
кон
процедура ЛИНИЯ
если впереди НЕ стена
то
шаг
делай ЛИНИЯ
шаг
иначе
поворот
поворот
поворот
шаг
шаг
поворот
поворот
поворот
все
конец процедуры
4. Составьте программу с рекурсивной процедурой, по которой исполнитель, находящийся в произвольной точке поля, дойдет до стенки, затем повернется на 90 градусов по часовой стрелке и дойдет до конца этой стенки вдоль нее. В результате будет нарисован угол.


