Уроки 58 - 61
Сортировка массива
(§ 21. Сортировка массива)
Составление программы на Паскале сортировки массива
Тест по теме «Программное управление работой компьютера»

Содержание урока

§ 21. Сортировка массива. Алгоритм сортировки методом пузырька

§ 21. Сортировка массива. Программа на Паскале сортировки методом пузырька

Компьютерный практикум ЦОР. Сортировка массива (Задание 1 - 4)

Компьютерный практикум ЦОР. Сортировка массива (Задание 5 - 8)

Тест по теме «Программное управление работой компьютера»

§ 21. Сортировка массива
Алгоритм сортировки методом пузырька

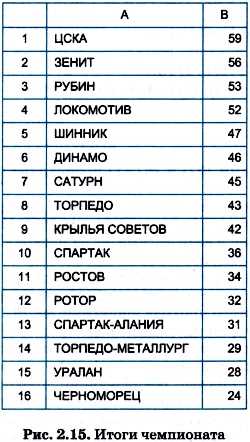
Известно, что данные в электронной таблице можно сортировать по возрастанию или убыванию значений в столбцах. Для задачи с таблицей футбольного чемпионата естественным действием была бы сортировка по убыванию значений набранных очков. Тогда вверху таблицы останется победитель чемпионата, а в нижней строчке — команда, занявшая последнее место. На рисунке 2.15 показана такая отсортированная таблица. Из нее мы получаем исчерпывающую информацию об итогах чемпионата: кто какое место занял.

Алгоритм сортировки методом пузырька

Рассмотрим, как программируется сортировка массива. Для решения этой задачи существует целый класс алгоритмов» Мы рассмотрим здесь только один из них, известный под названием «метод пузырька». Откуда такое название, станет ясно немного позже.

Проиллюстрируем идею метода пузырька на маленьком массиве из пяти чисел. Пусть это будет массив В[ 1:5], исходные значения в котором распределены случайным образом (рис. 2.16). Требуется отсортировать числа по убыванию.

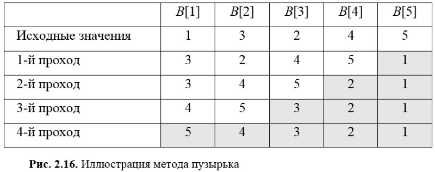
Первый этап (первый проход). Последовательно сравниваются пары соседних чисел и упорядочиваются по убыванию. Сначала сравниваются B[1] и В[2]. Поскольку на втором месте должно стоять меньшее число, то числа меняются местами. В[1] становится равным 3, В[2] — равным 1. Затем упорядочиваются В[2] и В[3]. Их значения тоже переставляются: В[2]=2, В[3]=1. Затем упорядочиваются В[3] и В[4]. И наконец, В[4] и В[5]. В результате первого прохода минимальное число попадает на свое место: В[5]=1.

Алгоритм первого прохода можно описать так:

Обмен значениями В[I] и В[I+1] происходит через третью переменную X.

Вот теперь можно понять смысл образа пузырька! В результате прохода минимальное значение «всплывает» в конец массива, как воздушный пузырек в воде всплывает на поверхность, подталкиваемый архимедовой силой.

Далее нужно повторять такие проходы еще три раза. После второго прохода на своем месте окажется В[4], после третьего прохода — B[3]. После четвертого прохода упорядочатся В[2] и В[1]. Нетрудно понять, что при втором проходе не надо трогать В[5], т. е. цикл должен повторяться для I от 1 до 3. При третьем проходе — от 1 до 2. И наконец, на четвертом проходе — от 1 до 1, т. е. всего 1 раз.

Следовательно, циклы, реализующие проходы, сами должны циклически повторяться. Причем при каждом следующем повторении длина цикла должна уменьшаться на единицу.

Отсюда вывод: структура алгоритма должна представлять собой два вложенных цикла. 

Вот полный алгоритм сортировки массива В [1:16]:

Здесь переменная К играет роль номера прохода. Для массива длиной 16 такие проходы требуется повторить 15 раз. Длина каждого К-го прохода равна 16-К.