Уроки 112 - 114
Решение уравнений в табличных процессорах
§70. Решение уравнений

Содержание урока

Приближённые методы

Метод перебора

Метод деления отрезка пополам

Пример: полёт мяча

Использование табличных процессоров

Вопросы и задания

Задачи

Пример: полёт мяча

Для иллюстрации рассмотрим такую задачу: Вася бросает мяч со скоростью 12 м/с. Под каким углом к горизонту Васе нужно бросить мяч, чтобы попасть в мишень на высоте 4 м на расстоянии 10 м? В момент броска мяч находится на высоте 2 м (рис. 9.7).

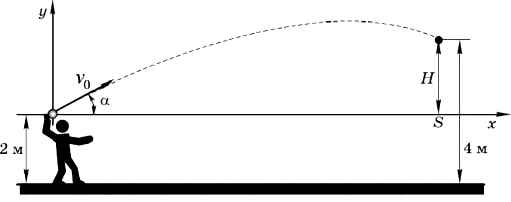
Рис. 9.7

Примем за начало координат точку, откуда вылетает мяч. Обозначим через v₀ начальную скорость мяча, через Н — разницу высот (Н = 4 - 2 = 2 м), а через S — расстояние до мишени (S = 10 м). Будем считать мяч материальной точкой; поскольку его скорость невысока, сопротивлением воздуха можно пренебречь. Известные из физики уравнения движения запишутся в виде:

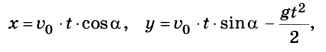
где g ≈ 9,81 м/с² — ускорение свободного падения. Задача сводится к тому, чтобы найти два неизвестных, t и а, при которых X = S и Y = H: 2

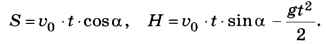
Время t можно сразу выразить из первого уравнения:

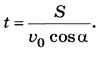
Подставляя этот результат во второе уравнение, получаем уравнение с одним неизвестным а, которое можно привести к стандартному виду f(a) = 0, где:

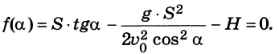
Решать его аналитически достаточно сложно ¹, поэтому мы найдём приближённое решение. При вычислении тригонометрических функций угол измеряется в радианах, поэтому нужно искать решение в диапазоне углов а от 0 до π/2.

---

¹ Хотя можно, например, с помощью замены z = 1 / cos²a

---

Мы не знаем, сколько решений имеет уравнение, поэтому изменим метод перебора так, чтобы найти все решения. Цикл while не будет останавливаться на первом найденном решении, а будет продолжаться, пока угол не станет больше π/2. Если в какой-то полосе есть решение, вычисляем угол в градусах и выводим его на экран. Приведём основные части программ на школьном алгоритмическом языке:

и на Паскале:

В переменной и хранится угол в радианах, а в переменной alpha — угол в градусах. Если запустить эту программу, мы увидим, что уравнение имеет два решение — углы примерно равны 35,6^o и 65,8^o.

Попробуйте применить в этой же задаче метод деления отрезка пополам. Подумайте, с какими проблемами мы здесь сталкиваемся, и почему они возникают.

Повторите вычисления для начальных скоростей 10 м/с и 20 м/с и объясните полученные результаты.

Следующая страница Использование табличных процессоров

Cкачать материалы урока