Уроки 119 - 120
Статистические расчеты. Условные вычисления
§73. Статистические расчеты
Содержание урока
Связь двух рядов данных
Связь двух рядов данных
Одна из задач обработки данных — установить взаимосвязь между величинами, процессами, явлениями. Пусть существуют два ряда данных одинаковой длины:
х1,х2,...,xn и y1,y2,...,yn.
Например, первый ряд — это температура воздуха за п последних дней, а второй ряд — значения атмосферного давления в те же дни. Требуется определить, есть ли связь между этими рядами, и оценить, насколько она сильная.
Для решения этой задачи чаще всего используется коэффициент корреляции (англ, correlation — взаимоотношение, связь):
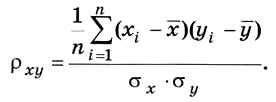
Здесь x и y — средние значения рядов, а σх и σy — их среднеквадратические отклонения.
Величина ρху — это безразмерный коэффициент 1, причём можно показать, что всегда -1≤ρху≤1. Если ρху>0, то увеличение значения х (в среднем) приводит к увеличению у; если же ρху<0, то при увеличении х значение у чаще всего уменьшается.
1 Попробуйте доказать это самостоятельно.
Чем больше модуль ρху, тем сильнее связь между двумя величинами. При ρху =-1 или ρху =1 они строго связаны линейной зависимостью y=kx + b, где k и b — некоторые числа. В случае ρху =-1 эта зависимость убывающая (k<0), а при ρху =1 — возрастающая (k>0).
Считается, что между х и у есть сильная связь, если |ρху| > 0,5. При меньших значениях ρху делать какие-то далеко идущие выводы не следует (связь слабая или не обнаружена).
Для вычисления коэффициента корреляции в табличных процессорах используется функция CORREL (КОРРЕЛ):
=CORREL(A1:A20;B1:B20) =КОРРЕЛ(А1:А20;В1:В20)
Обратите внимание, что у этой функции два аргумента (два ряда данных одинаковой длины), адреса двух диапазонов отделяются точкой с запятой.
Нужно учитывать, что коэффициент корреляции лучше всего обнаруживает линейную зависимость. Если связь есть, но она далека от линейной, коэффициент корреляции может быть невысок. В таких случаях для установления связи нужно использовать более сложные методы, которые мы здесь рассматривать не будем.
Следующая страница  Вопросы и задания
Вопросы и задания

