Уроки 13 - 14
Восьмеричная и шестнадцатеричная системы счисления
§12. Восьмеричная система счисления. §13. Шестнадцатеричная система счисления
Содержание урока
§12. Восьмеричная система счисления
§13. Шестнадцатеричная система счисления
Шестнадцатеричная система счисления
Алгоритм перевода шестнадцатеричного числа в двоичную систему счисления
Алгоритм перевода двоичного числа в шестнадцатеричную систему счисления
§13. Шестнадцатеричная система счисления
Алгоритм перевода двоичного числа в шестнадцатеричную систему счисления
1. Разбить двоичное число на тетрады, начиная справа.
В начало самой первой тетрады добавить слева нули, если это необходимо.
2. Перевести каждую тетраду (отдельно) в шестнадцатеричную систему счисления.
3. Соединить полученные цифры в одно «длинное» число.
Например: 10000100001010101111002 = 10 0001 0000 1010 1011 11002 = 210АВС16.
Шестнадцатеричная система оказалась очень удобной для записи значений ячеек памяти. Байт в современных компьютерах представляет собой 8 соседних битов, т. е. две тетрады. Таким образом, значение байтовой ячейки можно записать как две шестнадцатеричные цифры:
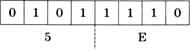
Каждый полубайт (4 бита) «упаковывается» в одну шестнадцатеричную цифру. Благодаря этому замечательному свойству, шестнадцатеричная система в сфере компьютерной техники практически полностью вытеснила восьмеричную1.
1 Начиная с 1964 года, когда шестнадцатеричная система стала широко использоваться в документации на новый компьютер IBM/360.
Перевод из шестнадцатеричной системы в восьмеричную (и обратно) удобнее выполнять через двоичную систему. Можно, конечно, использовать и десятичную систему, но в этом случае объём вычислений будет значительно больше.
При выполнении сложения нужно помнить, что в системе с основанием 16 перенос появляется тогда, когда сумма в очередном разряде превышает 15. Удобно сначала переписать исходные числа, заменив все буквы на их численные значения:
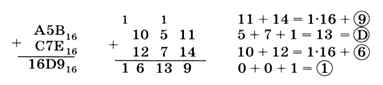
При вычитании заём из старшего разряда равен 1016 = 16, а все «промежуточные» разряды заполняются цифрой F — старшей цифрой системы счисления:
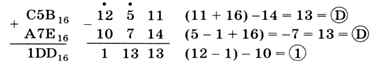
Если нужно работать с числами, записанными в разных системах счисления, их сначала переводят в какую-нибудь одну систему. Например, пусть требуется сложить 538 и 5616 и записать результат в двоичной системе счисления. Здесь можно выполнять сложение в двоичной, восьмеричной, десятичной или шестнадцатеричной системе. Переход к десятичной системе, а потом перевод результата в двоичную трудоёмок. Практика показывает, что больше всего ошибок делается при вычислениях в двоичной системе, поэтому лучше выбирать восьмеричную или шестнадцатеричную систему. Например, переведём число 538 в шестнадцатеричную систему через двоичную:
538 = 101 0112 = 10 10112 = 2В16.
Теперь сложим числа в 16-ричной системе:
2В16 + 5616 = 8116
и переведём результат в двоичную систему:
8116 = 1000 00012.
Следующая страница  Вопросы и задания
Вопросы и задания

