Уроки 92 - 94
Сортировка массивов
§64. Сортировка
Содержание урока
Метод пузырька (сортировка обменами)
«Быстрая сортировка»
«Быстрая сортировка»
Методы сортировки, описанные ранее, работают медленно для больших массивов данных (более 1000 элементов). Поэтому в середине XX века математики и программисты серьезно занимались разработкой более эффективных алгоритмов сортировки. Один из самых популярных «быстрых» алгоритмов, разработанный в 1960 г. английским учёным Чарльзом Хоаром, так и называется — «быстрая сортировка» (англ, quicksort).

Будем исходить из того, что сначала лучше делать перестановки элементов массива на большом расстоянии. Предположим, что у нас есть п элементов и известно, что они уже отсортированы в обратном порядке. Тогда за n/2 обменов можно отсортировать их как нужно — сначала поменять местами первый и последний, а затем последовательно двигаться с двух сторон к центру. Хотя это справедливо только тогда, когда порядок элементов обратный, подобная идея положена в основу алгоритма Quicksort.
Пусть дан массив А из n элементов. Выберем сначала наугад любой элемент массива (назовем его X). Обычно выбирают средний элемент массива, хотя это необязательно. На первом этапе мы расставим элементы так, что слева от некоторой границы находятся все числа, меньшие или равные X, а справа — большие или равные X:

Заметим, что элементы, равные X, могут находиться в обеих частях.
Теперь элементы расположены так, что ни один элемент из первой части при сортировке не окажется во второй части и наоборот. Поэтому далее достаточно отсортировать отдельно каждую часть массива. Такой подход называют «разделяй и властвуй» (англ, divide and conquer).
Лучше всего выбирать X так, чтобы в обеих частях было равное количество элементов. Такое значение X называется медианой массива. Однако для того, чтобы найти медиану, надо сначала отсортировать массив, т. е. заранее решить ту самую задачу, которую мы собираемся решить этим способом. Поэтому обычно в качестве X выбирают средний элемент массива.
Сначала будем просматривать массив слева до тех пор, пока не обнаружим элемент, который больше X (и, следовательно, должен стоять справа от X). Затем просматриваем массив справа до тех пор, пока не обнаружим элемент, меньший X (он должен стоять слева от X). Теперь поменяем местами эти два элемента и продолжим просмотр до тех пор, пока два «просмотра» не встретятся где-то в середине массива. В результате массив окажется разбитым на 2 части: левую со значениями, меньшими или равными X, и правую со значениями, большими или равными X. На этом первый этап («разделение») закончен. Затем такая же процедура применяется к обеим частям массива до тех пор, пока в каждой части не останется по одному элементу (таким образом, массив будет отсортирован).
Чтобы понять сущность метода, рассмотрим пример. Пусть задан массив:
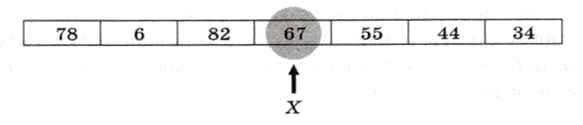
Выберем в качестве X средний элемент массива, т. е. 67. Найдем первый слева элемент массива, который больше или равен X и должен стоять во второй части. Это число 78. Обозначим индекс этого элемента через L. Теперь находим самый правый элемент, который меньше X и должен стоять в первой части. Это число 34. Обозначим его индекс через R:
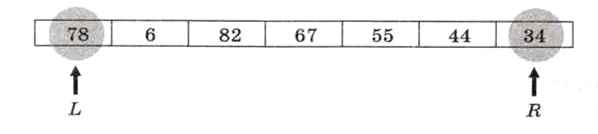
Теперь поменяем местами эти два элемента. Сдвигая переменную L вправо, a R — влево, находим следующую пару, которую надо переставить. Это числа 82 и 44:

Следующая пара элементов для переноски - числа 67 и 55:
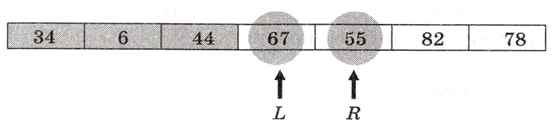
После этой перестановки дальнейший поиск приводит к тому, что переменная L становится больше R:

В результате все элементы массива, расположенные левее A[L], меньше или равны X, а все элементы правее А[R] — больше или равны X.
Теперь нужно применить тот же алгоритм к двум полученным частям массива: первая часть — с 1-го элемента до R-ro элемента, вторая часть — с L-ro до последнего элемента. Как вы знаете, такой приём называется рекурсией.
Чтобы не загромождать решение деталями оформления, которые сильно различаются в школьном алгоритмическом языке и в Паскале, предположим, что в нашей программе один глобальный массив А с индексами от 1 до N, который нужно сортировать. Термин «глобальный» означает, что массив доступен всем процедурам и функциям. Глобальные данные объявляются выше основной программы:

Тогда процедура сортировки принимает только два параметра, ограничивающие её «рабочую зону»: nStart — номер первого элемента, и nEnd — номер последнего элемента. Если nStart = nEnd, то в «рабочей зоне» один элемент и сортировка не требуется, т. е. нужно выйти из процедуры. В этом случае рекурсивные вызовы заканчиваются.
Приведём полностью процедуру быстрой сортировки на школьном алгоритмическом языке:

Для того чтобы отсортировать весь массив, нужно вызвать эту процедуру так:
qSort(l, N)
Скорость работы быстрой сортировки зависит от того, насколько удачно выбирается вспомогательный элемент X. Самый лучший случай — когда на каждом этапе массив делится на две равные части. Худший случай — когда в одной части оказывается только один элемент, а в другой — все остальные. При этом глубина рекурсии достигает N, что может привести к переполнению стека (нехватке стековой памяти).
Для того чтобы уменьшить вероятность худшего случая, в алгоритм вводят случайность: в качестве X на каждом шаге выбирают не середину рабочей части массива, а элемент со случайным номером:
X:=А[irand(L,R)]
В таблице 8.1 сравнивается время сортировки (в секундах) массивов разного размера, заполненных случайными значениями, с использованием трёх изученных алгоритмов.
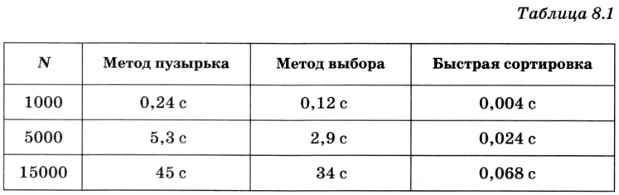
Как показывают эти данные, преимущество быстрой сортировки становится подавляющим при увеличении N.
Следующая страница  Вопросы и задания
Вопросы и задания

