Уроки 95 - 96
Двоичный поиск в массиве
§ 65. Двоичный поиск
Содержание урока
Двоичный поиск
Двоичный поиск
Ранее мы уже рассматривали задачу поиска элемента в массиве и привели алгоритм, который сводится к просмотру всех элементов массива. Такой поиск называют линейным. Для массива из 1000 элементов нужно сделать 1000 сравнений, чтобы убедиться, что заданного элемента в массиве нет. Если число элементов (например, записей в базе данных) очень велико, время поиска может оказаться недопустимым, потому что пользователь не дождётся ответа.
Как вы помните, основная задача сортировки — облегчить последующий поиск данных. Вспомним, как мы ищем нужное слово (например, слово «гравицапа») в словаре. Сначала открываем словарь примерно в середине и смотрим, какие там слова. Если они начинаются на букву «Л», то слово «гравицапа» явно находится на предыдущих страницах, и вторую часть словаря можно не смотреть. Теперь так же проверяем страницу в середине первой половины, и т. д. Такой поиск называется двоичным. Понятно, что он возможен только тогда, когда данные предварительно отсортированы. Для примера на рис. 8.12 показан поиск числа X = 44 в отсортированном массиве.
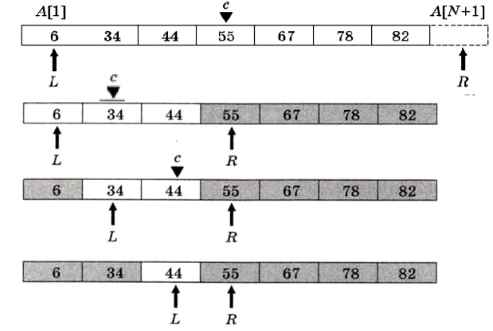
Рис. 8.12
Серым фоном выделены ячейки, которые уже не рассматриваются, потому что в них не может быть заданного числа. Переменные L и R ограничивают «рабочую зону» массива: L содержит номер первого элемента, a R — номер элемента, следующего за последним. Таким образом, нужный элемент (если он есть) находится в части массива, которая начинается с элемента A[L] и заканчивается элементом А[R-1].
На каждом шаге вычисляется номер среднего элемента «рабочей зоны», он записывается в переменную с. Если Х < А[с], то этот элемент может находиться только левее А[с], и правая граница R перемещается в с. В противном случае нужный элемент находится правее середины или совпадает с А[с]; при этом левая граница L перемещается в с.
Поиск заканчивается при выполнении условия L = R - 1, когда в рабочей зоне остаётся один элемент. Если при этом A[L] = X, то в результате найден элемент, равный X, иначе такого элемента нет.

Двоичный поиск работает значительно быстрее, чем линейный. В нашем примере (для массива из 8 элементов) удаётся решить задачу за 3 шага вместо 8 при линейном поиске. При увеличении размера массива эта разница становится впечатляющей. В таблице 8.2 сравнивается количество шагов для двух методов при разных значениях N.

Однако при этом нельзя сказать, что двоичный поиск лучше линейного. Нужно помнить, что данные необходимо предварительно отсортировать, а это может занять значительно больше времени, чем сам поиск. Поэтому такой подход эффективен, если данные меняются (и сортируются) редко, а поиск выполняется часто. Такая ситуация характерна, например, для баз данных.
Следующая страница  Вопросы и задания
Вопросы и задания

