Урок 4
Кодирование и декодирование
§5. Язык и алфавит. §6. Кодирование
Содержание урока
§5. Язык и алфавит
§6. Кодирование
Декодирование
§6. Кодирование
Декодирование
Декодирование — это восстановление информационного сообщения из последовательности кодов.
Например, закодированное сообщение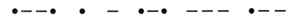 
можно восстановить, используя код Морзе «в обратную сторону»: в этой строке закодирована фамилия «Петров».
В некоторых случаях даже при использовании неравномерного кода не требуется вводить символ-разделитель. Для этого достаточно выполнение условия Фано: ни одно кодовое слово не совпадает с началом другого кодового слова. Такой код называют префиксным.
Пример 1. Пусть для кодирования первых 5 букв русского алфавита используется таблица:
Это неравномерный код, поскольку в нём есть двух- и трёхсимвольные кодовые слова. Построим для этой кодовой таблицы дерево, в котором от каждого узла (кроме листьев) отходят два ребра, помеченные цифрами 0 и 1. Чтобы найти код символа, нужно пройти по стрелкам от корня дерева к нужному листу, выписывая метки стрелок, по которым мы переходим (рис. 2.3).
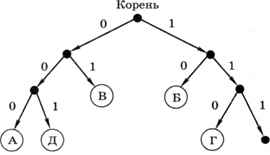
Рис. 2.3
Заметим, что ни один символ не лежит на пути от корня к другому символу. Это значит, что условие Фано выполняется и любую правильную кодовую последовательность можно однозначно декодировать. Например, рассмотрим цепочку 1100000100110. Букв с кодами 1 и 11 в таблице нет, поэтому сообщение начинается с буквы Г — она имеет код 110:
Следующий (единственно возможный) код — 000, это буква А:
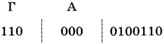
Аналогично декодируем всё сообщение:
Пример 2. Рассмотрим другую кодовую таблицу:
Здесь условие Фано не выполняется, поскольку код буквы Б (01) является началом кода буквы Г (011), а код буквы Д (100) начинается с кода буквы В (10). Дерево для этой кодовой таблицы выглядит так (рис. 2.4).
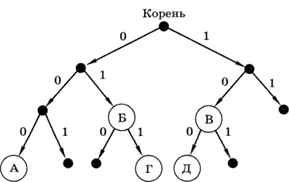
Рис. 2.4
Тем не менее можно заметить, что выполнено «обратное» условие Фано: ни одно кодовое слово не совпадает с окончанием другого кодового слова (такой код называют постфиксным). Поэтому закодированное сообщение можно однозначно декодировать с конца. Например, рассмотрим цепочку 011000110110. Последней буквой в этом сообщении может быть только В (код 10):
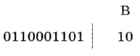
Вторая буква с конца — Б (код 01):
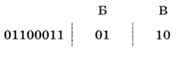
И так далее:
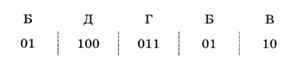
В общем случае (если код не является ни префиксным, ни постфиксным) декодировать сообщение удаётся только перебором вариантов.
Пример 3. Декодируем сообщение 010100111101, закодированное с помощью кодовой таблицы:
Здесь не выполняется ни «прямое», ни «обратное» условие Фано, поэтому декодировать сообщение однозначно, возможно, не удастся. На первом месте может быть буква А или буква Б. Сначала предположим, что это буква А:
А0100111101
Тогда второй буквой также может быть буква А:
АА00111101.
Дальше декодировать не получается, потому что в таблице нет кодов 0, 00 и 001. Поэтому проверяем второй вариант: вторая буква — Б:
АБ0111101.
Третьей буквой может быть А:
АБА11101,
Тогда четвёртая и пятая буквы определяются однозначно — это буквы Г и Д. Таким образом, один из подходящих вариантов — АБАГД.
Посмотрим, есть ли другие варианты. После сочетания АБ может стоять буква В:
АБВ1101,
тогда оставшиеся буквы — это ГА, а полное сообщение — АБВГА. Этот вариант тоже подходит.
Кроме того, на первом месте может стоять буква Б:
Б100111101,
но дальше декодировать не удаётся, потому что в таблице нет кодов 1, 10 и 100. Таким образом, сообщение может быть декодировано двумя способами: АБАГД и АБВГА.
Пример 3 показывает, что неоднозначное декодирование возможно тогда, когда начало кода одной буквы совпадает с концом кода другой и можно переместить границу между кодами букв в сообщении. Например, последовательность 01011 может быть декодирована как АВ (01011) и БГ (01011). Следовательно, нужно обратить внимание на те цепочки, которые встречаются как в начале, так и в конце кодовых слов.
Покажем, как найти сообщения, которые декодируются неоднозначно. Для таблицы из примера 3 построим граф Ал. А. Маркова следующим образом.
1. Определим все последовательности., которые совпадают с началом какого-то кодового слова и одновременно с концом какого-то кодового слова; в данном случае это две последовательности:
0 (начало кода буквы А и конец кода буквы Б)
1 (начало кода буквы Г и конец кода буквы Д)
10 (начало кода буквы Д и конец кода буквы Б).
2. Добавим к этому множеству {0, 1, 10} пустую строку, которую обычно обозначают буквой Λ (прописная греческая буква «лямбда»); элементы полученного множества {Λ, 0, 1} становятся узлами графа (рис. 2.5).
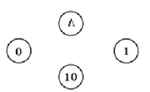
Рис. 2.5
3. Соединим узлы дугами (направленными рёбрами) по такому правилу: два узла X и Y соединяются дугой, если последовательная запись кода узла X, кода некоторой буквы (или нескольких букв) и кода узла Y даёт код ещё одной буквы (рис. 2.6).
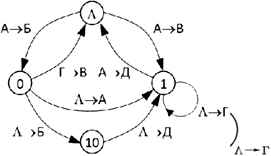
Рис. 2.6
Например, последовательная запись пустой строки (Λ), кода буквы А (01) и цепочки 0 даёт цепочку 010, которая совпадает с кодом буквы Б; поэтому рисуем дугу из вершины Λ в вершину 0; у этой дуги пишем А → Б, и т. д. Поскольку код буквы Г можно записать как 11 = 1Λ1, у вершины 1 появляется петля Λ → Г.
Любое сообщение декодируется однозначно тогда и только тогда, когда в полученном таким образом графе нет циклов, включающих вершину «Λ».
В нашем графе есть несколько таких циклов, например:
• цикл «Λ0Λ», соответствующий сообщению ΛА0ГΛ = 01011; это сообщение может быть расшифровано как АВ и как БГ;
• цикл «Λ1Λ», соответствующий сообщению ΛА1АΛ = 01101; это сообщение может быть расшифровано как АД и как ВА;
• цикл «Λ01Λ», соответствующий сообщению ΛА01АΛ = 01010Lj это сообщение может быть расшифровано как АДА и как БД;
• цикл «Λ0101Λ», соответствующий сообщению ΛА0101АΛ = 01010101; это сообщение может быть расшифровано как АБД и как БДА.
Кроме того, из-за петли у вершины 1 неоднозначно декодируется любая последовательность вида 01... 101, где многоточие обозначает любое количество единиц. Например, сообщение 0111101 может быть декодировано как АГД или ВГА (см. пример 3).
Пример 4. Существуют коды, для которых условия Фано не выполняются, но все сообщения однозначно декодируются. В кодовой таблице
код буквы А совпадает как с началом, так и с окончанием кода буквы В, т. е. этот код не является ни префиксным, ни постфиксным.
Проверим, можно ли однозначно декодировать сообщения, построенные с помощью такого кода. Множество последовательностей, которые совпадают с началом и концом кодовых слов, состоит из пустой строки и единицы: {А, 1}. Граф, построенный с помощью приведённого выше алгоритма, содержит два узла и одну петлю (рис. 2.7).
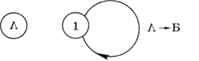
Рис. 2.7
В этом графе нет цикла, содержащего вершину А, поэтому любое сообщение, записанное с помощью такого кода, декодируется однозначно. Это можно показать и простыми рассуждениями:
1) все цепочки 11 в сообщении — это коды букв Б, иначе они не могут образоваться;
2) все цепочки 010 — это коды букв В;
3) остальные символы сообщения могут быть только нулями — это коды букв А.
Иногда при кодировании и декодировании происходит искажение сообщения. Например, известно, что перевод художественных текстов (особенно стихов) на другой язык и затем обратный перевод могут изменить их до неузнаваемости.
Следующая страница 
Вопросы и задания
Cкачать материалы урока
