Урок 5
Дискретность. Алфавитный подход к оценке количества информации
§7. Дискретность. §8. Алфавитный подход к оценке количества информации

Содержание урока

§7. Дискретность

Аналоговые и дискретные сигналы

Дискретизация

Вопросы и задания

§8. Алфавитный подход к оценке количества информации

§7. Дискретность

Дискретизация

Поскольку данные в компьютерах передаются с помощью дискретных сигналов, компьютеры могут хранить и обрабатывать только дискретную информацию, т. е. такую, которая может быть записана с помощью конечного количества знаков некоторого алфавита. Поэтому для ввода любых данных в компьютер их нужно перевести в дискретный код.

Дискретность означает, что мы представляем нечто целое (непрерывное) в виде набора отдельных элементов. Например, картина художника — это аналоговая (непрерывная) информация, а мозаика, сделанная на её основе (рисунок из кусочков разноцветного стекла), — дискретная. Множество вещественных чисел непрерывно (между любыми двумя различными числами есть ещё бесконечно много других), а множество целых чисел дискретно.

Дискретизация — это представление единого объекта в виде множества отдельных элементов.

Всем известное иррациональное число л содержит бесконечное количество знаков в дробной части. Если мы хотим записать, чему равно π, необходимо остановиться на каком-то знаке, отбросив остальные, например: π ≈ 3,14. Таким образом, мы перешли к дискретной информации, потому что рассматриваем только числа с шагом 0,01 — точки на числовой оси (рис. 2.10).

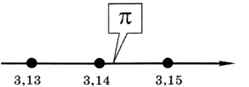
Рис. 2.10

Изменение высоты столбика термометра — это аналоговая информация, а записанная температура, округлённая до десятых долей градуса (например, 36,6°), — дискретная (рис. 2.11).

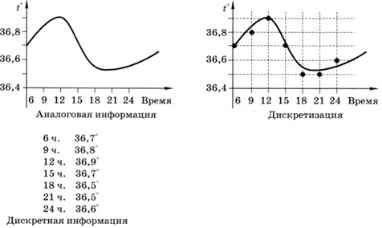
Рис. 2.11

Дискретность состоит в том, что записанные значения температуры изменяются скачкообразно (через 0,1°), — это дискретизация по уровню, или квантование. Кроме того, обычно температуру больного измеряют не непрерывно, а несколько раз в день — появляется дискретизация по времени.

Заметим, что при дискретизации, как правило, происходит потеря информации. В данном случае мы, во-первых, потеряли информацию об изменении температуры между моментами измерений и, во-вторых, исказили измеренные значения, округлив их до десятых (каждая дискретизация, и по времени, и по уровню, вносит свою ошибку). Чтобы уменьшить ошибки, нужно уменьшить шаг дискретизации — измерять температуру чаще, записывать показания термометра до тысячных долей градуса. Однако в любой практической задаче есть некоторый предел, после которого увеличение точности уже никак не влияет на конечный результат.

Из приведённого примера понятно, что непрерывность или дискретность — это не свойство самой информации, а свойство её представления. В данном случае информация — это сведения об изменении температуры человека в течение дня. Если бы температура измерялась постоянно и записывалась самописцем (в виде графика), можно было бы говорить о том, что информация представлена в аналоговой (непрерывной) форме.

Ещё один пример — аналоговые («стрелочные») и цифровые вольтметры, которые измеряют одну и ту же величину, но выводят результат измерения в разном виде (рис. 2.12).

Рис. 2.12

Теперь подумаем, как записать аналоговую величину, которая может принимать бесконечное множество значений. Вы уже знаете, что с помощью алфавита, состоящего из N символов, можно закодировать Q = разных сообщений длины L. Поэтому теоретически для записи аналоговой величины придется использовать бесконечное число знаков.

Итак, когда мы хотим записать (зафиксировать) информацию с помощью какого-то алфавита, нужно переходить к дискретному представлению. С одной стороны, это делает более надёжной передачу данных (если обе стороны одинаково понимают используемые знаки). С другой стороны, при дискретизации часть информации теряется.

Хотя аналоговую информацию невозможно точно представить в дискретном виде, при увеличении точности дискретизации свойства непрерывной и дискретной информации практически совпадают. Например, для точной записи числа тг требуется бесконечное количество цифр, но в расчётах чаще всего достаточно знать это значение с точностью не более 10 знаков.

Идеальная непрерывность существует только в теории. Мы считаем дерево, пластмассу, металл непрерывными, но на самом деле они состоят из отдельных молекул, расположенных на некотором расстоянии друг от друга, — это значит, что вещество дискретно. Иллюстрация в книге кажется нам сплошной, но при сильном увеличении видно, что она строится из отдельных точек (имеет «растр») (рис. 2.13).

Рис. 2.13

«Плёночная» фотография считается аналоговой, но при увеличении снимка с фотоплёнки нельзя бесконечно получать все новые и новые детали — предел «уточнения» определяется величиной зерна светочувствительного материала.

Мы часто воспринимаем дискретные объекты как непрерывные, потому что наши органы чувств не позволяют различить отдельные элементы. Например, разрешающая способность глаза составляет около одной угловой минуты (1' = 1/60 часть градуса), это значение определяется размером элементов сетчатки глаза. Поэтому человек не может различить два объекта, если направления на них различаются меньше, чем на 1'. Для того чтобы повысить разрешающую способность при наблюдении, применяют специальные приборы (например, бинокли и микроскопы).

Следующая страница Вопросы и задания

Cкачать материалы урока