Урок 6
Системы счисления. Позиционные системы счисления. Двоичная система счисления
§9. Системы счисления. §10. Позиционные системы счисления. §11. Двоичная система счисления
Содержание урока
§9. Системы счисления
Система счисления
§10. Позиционные системы счисления
§11. Двоичная система счисления
§9. Системы счисления
Система счисления
Система счисления — это правила записи чисел с помощью специальных знаков — цифр, а также соответствующие правила выполнения операций с этими числами.
Первоначально люди считали на пальцах — это самый простой способ, который используется и сейчас. Один загнутый (или отогнутый) палец обозначал единицу (один день, одного человека, одного барана и т. п.). Такая система счисления называется унарной (от лат. unus — один). В качестве цифр унарной системы можно использовать камешки, узелки, счётные палочки (как в начальной школе), зарубки на дереве (как делал Робинзон Крузо) или на кости, чёрточки на бумаге, точки и другие одинаковые знаки или предметы.
С помощью унарной системы можно записывать только натуральные числа, причём запись больших чисел получается очень длинной (представьте себе, как записать миллион). Цифра любой позиции числа, записанного в унарной системе, всегда обозначает единицу, поэтому это одна из непозиционных систем счисления.
Непозиционная система счисления — это такая система счисления, в которой значение цифры не зависит от её места в записи числа.
К непозиционным относится и десятичная египетская система счисления. Египтяне ввели 7 знаков-иероглифов, которые обозначали степени числа 10 (чёрточка, хомут, верёвка, лотос, палец, лягушка, человек) (рис. 2.14).
Рис. 2.14
В этой системе, например, число 235 записывалось как 
В римской системе счисления (она также считается непозиционной) в качестве цифр используются латинские буквы: I обозначает 1, V — 5, X — 10, L — 50, С — 100, D — 500, М — 1000. Единицы, десятки, сотни и тысячи кодировались отдельными группами, например:
2368 = 2000 + 300 + 60 + 8 = (1000 + 1000) + (100 + 100 + 100) + (50 + 10) + (5 + 1 -I- 1 + 1) = MMCCCLXVIII.
Больше трёх одинаковых цифр подряд не ставили, поэтому число 4 записывали как IV. В такой записи меньшая цифра (I) стоит перед большей (V), поэтому она вычитается из неё. То есть:
IV = 5 - 1 = 4.
Аналогично записывались числа 9, 40, 90, 400 и 900:
IX = 10 - 1 = 9, XL = 50 - 10 = 40, ХС = 100 - 10 = 90,
CD = 500 - 100 = 400, СМ = 1000 - 100 = 900.
Из-за этой особенности римскую систему нельзя считать полностью непозиционной, потому что значение меньшей цифры, стоящей слева от большей, меняется на отрицательное.
У римской системы есть несколько серьёзных недостатков:
• можно записывать только натуральные числа (что делать с дробными и отрицательными?);
• чтобы записывать большие числа, необходимо вводить всё новые и новые цифры (иногда использовались цифры с подчёркиванием или чертой сверху, что обозначало увеличение в 1000 раз: V — 5000, X — 10 000 и т. д.);
• сложно выполнять арифметические действия.
Сейчас римская система применяется для нумерации веков (XXI век), месяцев, глав в книгах, на циферблатах часов (например, на Спасской башне Московского Кремля).
В славянской системе счисления в качестве цифр использовались буквы алфавита, над которыми ставился знак 
(«титло») (рис. 2.15).
Рис. 2.15
Если в ряду стояло несколько цифр, знак «титло» ставился только у первой. Старшие цифры записывались справа от младших, например, число 11 записывалось как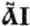 
. Славянская система счисления используется на циферблате часов Суздальского кремля.
Следующая страница 
Вопросы и задания
Cкачать материалы урока
