Урок 6
Системы счисления. Позиционные системы счисления. Двоичная система счисления
§9. Системы счисления. §10. Позиционные системы счисления. §11. Двоичная система счисления
Содержание урока
§9. Системы счисления
§10. Позиционные системы счисления
Основные понятия
§11. Двоичная система счисления
§10. Позиционные системы счисления
Основные понятия
Позиционная система счисления — это такая система счисления, в которой значение цифры («вес») полностью определяется её местом (позицией) в записи числа.
Пример позиционной системы счисления — привычная нам десятичная система. В числе 6375 цифра 6 обозначает тысячи (т. е. 6000), цифра 3 — сотни (300), цифра 7 — десятки (70), а цифра 5 — единицы:
6375 = 6 • 1000 + 3 • 100 + 7 • 10 + 5 • 1.
Алфавит системы счисления — это используемый в ней набор цифр.
Основание системы счисления — это количество цифр в алфавите (мощность алфавита).
В десятичной системе основание — 10, алфавит состоит из 10 цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9. Число 10, вероятно, было выбрано потому, что люди сначала использовали для счета свои 10 пальцев на руках.
Разряд — это позиция цифры в записи числа. Разряды в записи целых чисел нумеруются с нуля справа налево.
В числе 6375 цифра 6 стоит в третьем разряде (тысячи, 103), 3 — во втором разряде (сотни, 102), 7 — в первом (десятки, 101), а 5 — в нулевом (единицы, 100). Не забывайте, что любое число (кроме нуля!) в нулевой степени равно 1. Поэтому
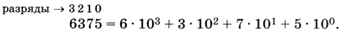
Это так называемая развёрнутая форма записи числа. Из этой записи видно, что последняя цифра 5 — это остаток от деления числа на 10 (все остальные слагаемые делятся на 10); число, составленное из двух последних цифр (75), — это остаток от деления исходного числа на 100 = 102 и т. д. Поэтому все числа, делящиеся на 100 без остатка, оканчиваются на два нуля.
Чтобы определить число, записанное в позиционной системе счисления, нужно значение каждой цифры умножить на основание системы счисления в степени, равной разряду этой цифры, и сложить полученные величины.
Число 6375 можно представить в другой форме — по схеме Горнера:
6375 = ((6 • 10 + 3) • 10 + 7) • 10 + 5.
Эта форма позволяет найти число, используя только умножение и деление (без возведения в степень).
Кроме десятичной системы на практике используются ещё несколько позиционных систем:
• двоичная, восьмеричная и шестнадцатеричная в компьютерной технике;
• двенадцатеричная английская система мер (1 фут =12 дюймов, 1 шиллинг = 12 пенсов);
• шестидесятеричная система измерения времени (1 час = = 60 минут, 1 минута = 60 секунд).
Следующая страница 
Целые числа
Cкачать материалы урока
