Урок 6
Системы счисления. Позиционные системы счисления. Двоичная система счисления
§9. Системы счисления. §10. Позиционные системы счисления. §11. Двоичная система счисления
Содержание урока
§9. Системы счисления
§10. Позиционные системы счисления
Целые числа
§11. Двоичная система счисления
§10. Позиционные системы счисления
Целые числа
Теперь можно записать аналогичные выражения для системы счисления с любым натуральным основанием р > 1. Её алфавит состоит из р цифр 1 от 0 до р — 1, т. е. «старшая» (наибольшая) цифра в позиционной системе счисления на единицу меньше, чем основание.
1 При р > 10 используются также и латинские буквы, но об этом далее.
Рассмотрим четырёхзначное число а3а2а1а0, записанное в системе счисления с основанием р. Здесь а3, а2, а1 и а0 — отдельные цифры, стоящие соответственно в третьем, втором, первом и нулевом разрядах. Это число может быть записано в развёрнутой форме:
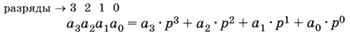
или с помощью схемы Горнера:
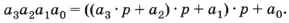
Оба способа можно использовать для перевода числа из любой позиционной системы в десятичную систему. Например, пусть число 12345 записано в пятеричной системе счисления (с основанием 5). Нижний индекс 5 в записи 12345 обозначает основание системы счисления (для десятичной системы основание не указывают). Тогда:
12345 = 1 • 53 + 2 • 52 + 3 • 51 + 4 • 50 = 125 + 2 • 25 + 3 • 5 + 4 = 194,
12345 = ((1-5 +2)- 5 + 3)- 5 + 4 = (7- 5 + 3)- 5 + 4 = 38- 5 + 4 = 194.
Схема Горнера очень удобна для обработки данных при вводе чисел с клавиатуры, когда цифры числа вводятся последовательно, начиная с первой, и их количество заранее неизвестно.
Развёрнутую запись числа можно использовать для обратного перехода, от десятичной системы к системе с основанием р. Действительно, из формулы
а3а2a1а0 = а3 • р3 + а2 • p2 + а1 • p + а0 следует, что а0 — это остаток от деления исходного числа на основание р. Если мы разделим исходное число на р и отбросим остаток, мы получим:
а3а2а1 = а3 • p2 + а2 • p + а1.
Теперь легко найти а1 — это последняя цифра получившегося числа, которая, как мы знаем, равна остатку от его деления на р. Разделив новое получившееся число на р и отбросив остаток, получим число
а3а2 = а3 • p + а2.
из которого найдём а2 как остаток от деления на р. Разделив на р ещё раз, получаем последнюю цифру а3.
Переведём, например, число 194 в пятеричную систему счисления (р = 5). Найдём остаток от деления на 5:
194 = 38-5 + 4.
Таким образом, мы нашли последнюю цифру — 4. Частное равно 38, повторяем ту же операцию:
38 = 7 • 5 + 3.
Следующая (с конца) цифра числа — 3. Дальше получаем:
7 = 1 • 5 +2,
третья с конца цифра — 2, а четвёртая — 1 (единица уже не делится на 5). Обратим внимание, что с помощью этого способа мы находим цифры числа, начиная с последней.
Поэтому полученные остатки нужно выписать в обратном порядке:
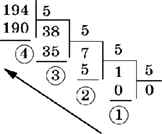
Ответ: 12345.
Для перевода числа из десятичной системы в систему счисления с основанием р нужно делить число на р, отбрасывая остаток на каждом шаге, пока не получится 0. Затем надо выписать найденные остатки в обратном порядке.
Можно было заметить, что такой алгоритм фактически использует схему Горнера, «раскручивая» её в обратном порядке. При каждом делении частное и остаток определяются однозначно, поэтому представление числа в любой позиционной системе единственно.
Рассмотренные приёмы позволяют записать любое неотрицательное число в заданной позиционной системе счисления. Признаком отрицательного числа служит знак «-», после которого по тем же правилам записывается модуль числа.
Пример 1. Зная десятичное число и его запись в некоторой позиционной системе счисления, можно найти основание этой системы. Пусть, например, число 71 в некоторой системе с основанием х записывается как 56х. Представим это число в развёрнутой форме:
71 = 56х = 5 • х1 + 6 • х0 = 5 • х + 6.
Решая уравнение 71 = 5 • х + 6 относительно неизвестного х, получаем: х = 13. Значит, искомое основание системы — 13.
Пример 2. В более сложных случаях может получиться алгебраическое уравнение второй (или ещё более высокой) степени. Например, пусть то же число 71 в некоторой системе с основанием х записывается как 155х. Представим это число в развёрнутой форме:
71 = 155х = 1 • х2 + 5 • х1 + 5 • х0 = х2 + 5 • х + 5.
Решая уравнение 71 = х2 + 5х + 5 относительно неизвестного х, получаем два решения: х1 = -11 и х2 = 6. Искомое основание положительно, поэтому правильный ответ — 6.
Пример 3. Если запись числа в системе счисления задана не полностью, решений может быть несколько. Например, найдём все основания систем счисления, в которых запись десятичного числа 24 оканчивается на 3. Здесь удобно использовать схему Горнера, из которой сразу следует
24 = k • х + 3,
где х — неизвестное основание системы счисления, k — некоторое натуральное число или 0. Отсюда сразу получаем 21 — k • х, т. е. все интересующие нас основания являются делителями числа 21. Это могут быть 3, 7 и 21. Поскольку последняя цифра числа — 3, основание не может быть равно 3 (в троичной системе нет цифры 3), поэтому условию задачи удовлетворяют только основания 7 и 21.
Пример 4. Найдём все десятичные числа, не превосходящие 40, запись которых в системе счисления с основанием 4 оканчивается на 11. Используя схему Горнера, находим, что все интересующие нас числа имеют вид
N = k • 42 + 1 • 4+1 = k • 16 + 5, где k — некоторое натуральное число или 0. Подставляя k = 0, 1, 2, 3,..., находим соответствующие числа N = 5, 21, 37, 53,.... Из них только 5, 21 и 37 удовлетворяют условию (не больше 40).
Пример 5. Все 5-буквенные слова, составленные из букв А, О, У, записаны в алфавитном порядке. Вот начало списка:
1. ААААА
2. ААААО
3. ААААУ
4. АААОА
Найдём слово, которое стоит на 140-м месте от начала списка.
Как ни странно, эта задача прямо связана с позиционными системами счисления. В словах используется набор из трёх разных символов, для которых задан порядок (алфавитный). Заменив буквы А, О и У соответственно на цифры 0, 1 и 2, выпишем начало списка:
1. 00000
2. 00001
3. 00002
4. 00010
Это числа, записанные в троичной системе счисления в порядке возрастания. Тогда легко понять, что на 140-м месте от начала списка стоит десятичное число 139, записанное в троичной системе счисления:
139 = 120113.
Заменив обратно цифры на буквы, получаем ответ: 12011 → ОУАОО.
Следующая страница 
Вопросы и задания
Cкачать материалы урока
