Урок 6
Системы счисления. Позиционные системы счисления. Двоичная система счисления
§9. Системы счисления. §10. Позиционные системы счисления. §11. Двоичная система счисления

Содержание урока

§9. Системы счисления

§10. Позиционные системы счисления

Основные понятия

Целые числа

Вопросы и задания

Задачи

Дробные числа

Вопросы и задания

Задачи

§11. Двоичная система счисления

§10. Позиционные системы счисления

Дробные числа

Дробные числа сначала рассмотрим на примере десятичной системы. Число 0,6375 можно представить в виде:

0,6375 = 6 • 0,1 + 3 • 0,01 + 7 • 0,001 + 5 • 0,0001.

Все множители, на которые умножаются значения цифр, представляют собой отрицательные степени числа 10 — основания системы счисления. То есть можно использовать развёрнутую форму записи, вводя отрицательные разряды:

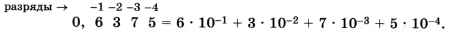
Это число можно представить также с помощью схемы Горнера:

0,6375 = 101 • (6 + 101 • (3 + 10-1 • (7 + 101 • 5))).

Рассмотрим дробное число 0,а₁а₂а₃а₄, записанное в системе счисления с основанием р. Здесь а₄, а₂, а₃, а₄ — это отдельные цифры, стоящие соответственно в разрядах -1, -2, -3 и -4. Это число может быть записано в развёрнутой форме

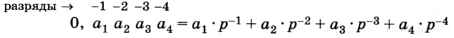
или с помощью схемы Горнера:

0,а₁а₂а₃а₄ = р^-1 • (а₁ + р^-1 • (а₂ + р^-1 • (а₃ + р^-1 + a₄))).

Умножив это число на р, получаем а₁,а₂а₃а₄. Если взять целую часть результата, мы получим цифру а₁. Таким же способом можно найти оставшиеся цифры дробной части: на каждом шаге умножаем дробную часть на р и запоминаем целую часть результата — это и будет очередная цифра записи числа в системе с основанием р. Например, переведём число 0,9376 в пятеричную систему (табл. 2.2).

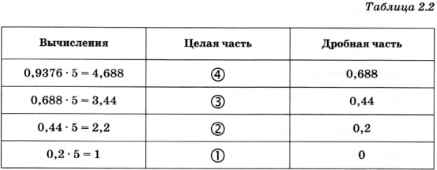
Чтобы получить ответ, нужно выписать все целые части результатов, полученные на каждом шаге:

0,9376 = 0,4321₅.

Вычисления заканчиваются, когда при очередном умножении дробная часть результата равна нулю. Это означает, что все остальные цифры дробной части — нули. В любом ли случае это произойдёт? К сожалению, нет. Чтобы убедиться в этом, вы можете попробовать перевести в пятеричную систему число 0,3 (должна получиться бесконечная дробь). Такая ситуация может случиться в любой системе счисления (например, вспомните, что число 1/3 записывается в виде бесконечной десятичной дроби). В этом случае обычно задают нужное количество значащих цифр и округляют число соответствующим образом.

Если нужно перевести в некоторую систему счисления число, в котором есть целая и дробная части, эти части переводят отдельно, а потом соединяют. Например, переведём число 25,375 в шестеричную систему:

25,375 = 25 + 0,375,

25 = 41₆, 0,375 = 0,213₆ ⇒ 25,375 = 41,213₆.

Следующая страница Вопросы и задания

Cкачать материалы урока