Уроки 5 - 7
Измерение информации (§§ 3 - 4)

Содержание урока

Измерение информации. Алфавитный подход

Измерение информации. Содержательный подход

Практическая работа № 1.2 "Измерение информации"

Измерение информации
Алфавитный подход

Вопрос об измерении количества информации является очень важным как для науки, так и для практики. В самом деле, если информация является предметом нашей деятельности, мы ее храним, передаем, принимаем, обрабатываем. Поэтому важно договориться о способе ее измерения, позволяющем, например, ответить на вопросы: достаточно ли места на носителе, чтобы разместить нужную нам информацию, или сколько времени потребуется, чтобы передать ее по имеющемуся каналу связи. Величина, которая нас в этих ситуациях интересует, называется объемом информации. В таком случае говорят об алфавитном, или объемном, подходе к измерению информации.

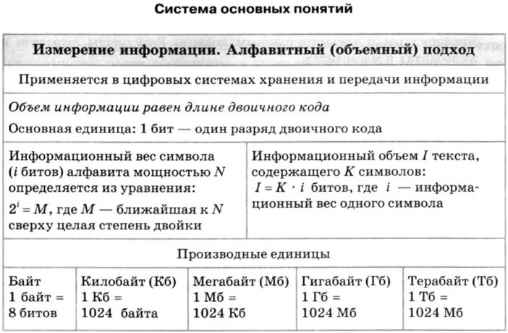
Алфавитный подход к измерению информации применяется в цифровых (компьютерных) системах хранения и передачи информации. В этих системах используется двоичный способ кодирования информации. При алфавитном подходе для определения количества информации имеет значение лишь размер (объем) хранимого и передаваемого кода. Алфавитный подход еще называют объемным подходом. Из курса информатики 7-9 классов вы знаете, что если с помощью i-разрядного двоичного кода можно закодировать алфавит, состоящий из N символов (где N — целая степень двойки), то эти величины связаны между собой по формуле:

2ⁱ = N.

Число N называется мощностью алфавита.

Если, например, i = 2, то можно построить 4 двухразрядные комбинации из нулей и единиц, т. е. закодировать 4 символа. При i = 3 существует 8 трехразрядных комбинаций нулей и единиц (кодируется 8 символов):

Английский алфавит содержит 26 букв. Для записи текста нужны еще как минимум шесть символов: пробел, точка, запятая, вопросительный знак, восклицательный знак, тире. В сумме получается расширенный алфавит мощностью в 32 символа.

Поскольку 32 = 2⁵, все символы можно закодировать всевозможными пятиразрядными двоичными кодами от 00000 до 11111. Именно пятиразрядный код использовался в телеграфных аппаратах, появившихся еще в XIX веке. Телеграфный аппарат при вводе переводил английский текст в двоичный код, длина которого в 5 раз больше, чем длина исходного текста.

В двоичном коде каждая двоичная цифра несет одну единицу информации, которая называется 1 бит.

Бит является основной единицей измерения информации.

Длина двоичного кода, с помощью которого кодируется символ алфавита, называется информационным весом символа. В рассмотренном выше примере информационный вес символа расширенного английского алфавита оказался равным 5 битам.

Информационный объем текста складывается из информационных весов всех составляющих текст символов. Например, английский текст из 1000 символов в телеграфном сообщении будет иметь информационный объем 5000 битов.

Алфавит русского языка включает 33 буквы. Если к нему добавить еще пробел и пять знаков препинания, то получится набор из 39 символов. Для двоичного кодирования символов такого алфавита пятиразрядного кода уже недостаточно. Нужен как минимум 6-разрядный код. Поскольку 2⁶ = 64, остается еще резерв для 25 символов (64 - 39 = 25). Его можно использовать для кодирования цифр, всевозможных скобок, знаков математических операций и других символов, встречающихся в русском тексте. Следовательно, информационный вес символа в расширенном русском алфавите будет равен 6 битам. А текст из 1000 символов будет иметь объем 6000 битов.

Итак, если i — информационный вес символа алфавита, а К — количество символов в тексте, записанном с помощью этого алфавита, то информационный объем I текста выражается формулой:

I = К x i (битов).

Идея измерения количества информации в сообщении через длину двоичного кода этого сообщения принадлежит выдающемуся российскому математику Андрею Николаевичу Колмогорову. Согласно Колмогорову, количество информации, содержащееся в тексте, определяется минимально возможной длиной двоичного кода, необходимого для представления этого текста.

Для определения информационного веса символа полезно знать ряд целых степеней двойки. Вот как он выглядит в диапазоне от 2¹ до 2¹⁰:

Поскольку мощность N алфавита может не являться целой степенью двойки, информационный вес символа алфавита мощности N определяется следующим образом. Находится ближайшее к N значение во второй строке таблицы, не меньшее чем N.

Соответствующее значение i в первой строке будет равно информационному весу символа.

Пример. Определим информационный вес символа алфавита, включающего в себя все строчные и прописные русские буквы (66); цифры (10); знаки препинания, скобки, кавычки (10). Всего получается 86 символов.

Поскольку 2⁶ < 86 < 2⁷, информационный вес символов данного алфавита равен 7 битам. Это означает, что все 86 символов можно закодировать семиразрядными двоичными кодами.

Для двоичного представления текстов в компьютере чаще всего применяется восьмиразрядный код. С помощью восьмиразрядного кода можно закодировать алфавит из 256 символов, поскольку 256 = 2⁸. В стандартную кодовую таблицу (например, используемую в ОС Windows таблицу ANSI) помещаются все необходимые символы: английские и русские буквы — прописные и строчные, цифры, знаки препинания, знаки арифметических операций, всевозможные скобки и пр.

Более крупной, чем бит, единицей измерения информации является байт: 1 байт = 8 битов.

Информационный объем текста в памяти компьютера измеряется в байтах. Он равен количеству символов в записи текста.

Одна страница текста на листе формата А4 кегля 12 с одинарным интервалом между строками в компьютерном представлении будет иметь объем 4000 байтов, так как на ней помещается примерно 4000 знаков.

Помимо бита и байта, для измерения информации используются и более крупные единицы:

1 Кб (килобайт) =	210 байтов = 1024 байта;
1 Мб (мегабайт) =	210 Кб	=	1024	Кб;
1 Гб (гигабайт)  =	210 Мб	= 1024 Мб;
1 Тб (терабайт) =	210 Гб	= 1024 Гб.

Объем той же страницы текста будет равен приблизительно 3,9 Кб. А книга из 500 таких страниц займет в памяти компьютера примерно 1,9 Мб.

В компьютере любые виды информации: тексты, числа, изображения, звуки — представляются в форме двоичного кода.

Объем информации любого вида, выраженный в битах, равен длине двоичного кода, в котором эта информация представлена.

Вопросы и задания

1. Есть ли связь между алфавитным подходом к измерению информации и содержанием информации?
2. В чем можно измерить объем письменного или печатного текста?
3. Оцените объем одной страницы данного учебника в байтах.
4. Что такое бит с позиции алфавитного подхода к измерению информации?
5. Как определяется информационный объем текста по А. Н. Колмогорову?
6. Какой информационный вес имеет каждая буква русского алфавита?
7. Какие единицы используются для измерения объема информации на компьютерных носителях?
8. Сообщение, записанное буквами из 64-символьного алфавита, содержит 100 символов. Какой объем информации оно несет?
9. Сколько символов содержит сообщение, записанное с помощью 16-символьного алфавита, если его объем составляет 1/16 Мб?
10. Сообщение занимает 2 страницы и содержит 1/16 Кб информации. На каждой странице 256 символов. Какова мощность используемого алфавита?
11. Возьмите страницу текста из данного учебника и подсчитайте информационные объемы текста, получаемые при кодировании его семиразрядным и восьмиразрядным кодами. Результаты выразите в килобайтах и мегабайтах.

Следующая страница Измерение информации. Содержательный подход