Уроки 26 - 27
Программирование циклов
Практикум
Практическая работа № 3.4
"Программирование циклических алгоритмов"

Содержание урока

Программирование циклов

Вложенные и итерационные циклы

Работа 3.4. Программирование циклических алгоритмов

Работа 3.4. Программирование циклических алгоритмов

Задание 1
Циклы с заданным числом повторений

Вычислить значение суммы или произведения числовой последовательности.

Уровень 1

1. Дано натуральное число N. Вычислить:

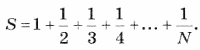
2. Дано натуральное число N. Вычислить:

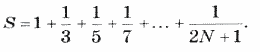
3. Дано натуральное число N. Вычислить:

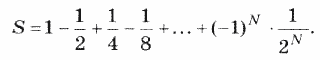
4. Дано натуральное число N. Вычислить:

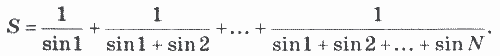
5. Дано натуральное число N. Вычислить произведение первых N сомножителей:

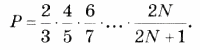
6. Дано натуральное n. Вычислить:

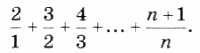
7. Вычислить:

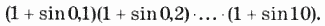
Уровень 2

8. Дано натуральное число N. Вычислить:

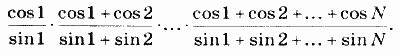
9. Дано действительное число х. Вычислить:

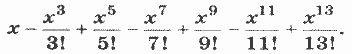
10. Даны натуральное n, действительное х. Вычислить:

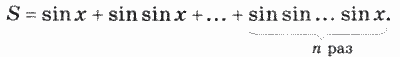
11. Дано действительное х. Вычислить:

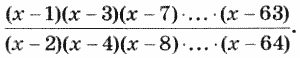
12. Дано натуральное n. Вычислить:

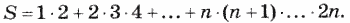
13. Дано натуральное число n. Вычислить:

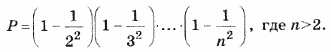
14. Вычислить по схеме Горнера:

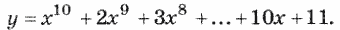
15. Числа Фибоначчи (f _n ) определяются формулами

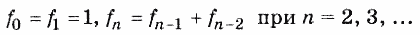
Для данного значения р определить f _p .

16. Даны натуральные числа n и k. Вычислить:

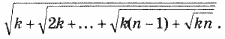
Задание 2
Итерационные циклы

Найти наименьший номер последовательности, заданной рекуррентной формулой, для которого выполняется условие |а_n - а_n-1| < ε, где ε — малая величина. Вывести на экран этот номер и все элементы a_i, где i = 1, 2, ..., n.

Задание 3
Циклы при обработке целых чисел

Решить поставленные задачи с помощью циклических алгоритмов (простых и вложенных), используя операции целочисленной арифметики.

Уровень 2

1. Натуральные числа а, b, с называются числами Пифагора, если выполняется условие а² + b² = с². Напечатать все числа Пифагора, меньшие N.

2. Найти наибольшую и наименьшую цифры в записи данного натурального числа.

3. Дано натуральное число N. Найти и вывести все числа в интервале от 1 до N - 1, у которых сумма всех цифр совпадает с суммой цифр данного числа. Если таких чисел нет, то вывести слово «нет».

Пример: N = 44. Числа: 17, 26, 35.

4. Дано натуральное число N. Найти и вывести все числа в интервале от 1 до N - 1, у которых произведение всех цифр совпадает с суммой цифр данного числа. Если таких чисел нет, то вывести слово «нет».

Пример: N = 44. Числа: 18, 24.

5. Дано натуральное число N (N > 9). Определить количество нулей, идущих подряд в младших разрядах данного числа.

Пример: N = 1020000. Количество нулей равно четырем.

6. Найти все натуральные числа, не превосходящие заданного n, которые делятся на каждую из своих цифр.

7. Дано натуральное число N. Получить новое число М, которое образуется из числа N путем замены последней цифры на наименьшую цифру в записи числа N.

Пример: N = 128452, М = 128451.

8. Дано натуральное число N. Получить новое число М, которое образуется из числа N путем замены последней цифры на наибольшую цифру в записи числа N.

Пример: N = 128452, М = 128458.

Уровень 3

9. Даны два натуральных числа m и n. Проверить, есть ли в записи числа m цифры, одинаковые с цифрами в записи числа n.

10. Дано натуральное число N (N > 9). Определить количество нулей в цифровой записи числа, кроме нулей в младших разрядах.

Пример: N = 10025000. Количество нулей равно двум.

11. Натуральное число М называется совершенным, если оно равно сумме всех своих делителей, включая 1, но исключая себя. Напечатать все совершенные числа, меньшие заданного числа N.

12. Дано целое n > 2. Напечатать все простые числа из диапазона [2, n].

13. Дано натуральное число N. Определить количество цифр в цифровой записи данного числа, которые имеют наименьшее значение.

Пример: N = 4548. Количество цифр с наименьшим значением равно двум (две цифры 4).

14. Дано натуральное число N. Определить количество цифр в цифровой записи данного числа, которые имеют наибольшее значение.

Пример: N = 1808. Количество цифр с наибольшим значением равно двум (две цифры 8).

15. Палиндром — это сочетания символов, которые читаются одинаково слева направо и справа налево. Например, числа 4884, 121 являются палиндромами. Составить программу, которая определяет, является ли заданное натуральное число палиндромом.

16. Дано натуральное число n. Переставить его цифры так, чтобы образовалось максимальное число, записанное теми же цифрами.

17. Дано натуральное число n. Переставить его цифры так, чтобы образовалось наименьшее число, записанное теми же цифрами.

Следующая страница Программирование циклов