Урок 4
Структура информации (простые структуры). Деревья. Графы
§4. Структура информации

Содержание урока

Зачем структурировать информацию?

Знакомые структуры данных

Иерархия (дерево)

Графы

Вопросы и задания

Задачи

Практическая работа № 1 «Оформление документа»

Практическая работа № 2 «Структуризация информации (таблица, списки)»

Практическая работа № 3 «Структуризация информации (деревья)»

Практическая работа № 4 «Графы»

Иерархия (дерево)

Линейных списков и таблиц иногда недостаточно для того, чтобы представить все связи между элементами. Например, в некоторой фирме есть директор, ему подчиняются главный инженер и главный бухгалтер, у каждого из них есть свои подчинённые. Если мы захотим нарисовать схему управления этой фирмы, она получится многоуровневой (рис. 1.11, а).

Такая структура, в которой одни элементы «подчиняются» другим, называется иерархией (от древнегреческого fepap%ta — священное правление). В информатике иерархическую структуру называют деревом. Дело в том, что, если перевернуть схему на рис. 1.11 вверх ногами, она становится похожа на дерево (точнее, на куст, см. рис. 1.11, б).

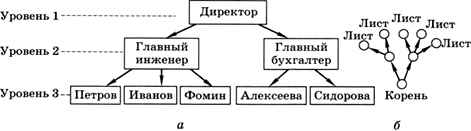
Рис. 1.11

Дерево состоит из узлов и связей между ними (они называются дугами). Самый первый узел, расположенный на верхнем уровне (в него не входит ни одна стрелка-дуга), — это корень дерева. Конечные узлы, из которых не выходит ни одна дуга, называются листьями. Все остальные узлы, кроме корня и листьев, — промежуточные.

Из двух связанных узлов тот, который находится на более высоком уровне, называется родителем, а другой — сыном. Корень — это единственный узел, у которого нет родителя; у листьев нет сыновей.

Используются также понятия предок и потомок. Потомок какого-то узла — это узел, в который можно перейти по стрелкам от узла-предка. Соответственно, предок какого-то узла — это узел, из которого можно перейти по стрелкам в данный узел.

В дереве на рис. 1.12 родитель узла Е — это узел В, а предки узла Е — это узлы А я В, для которых узел Е — потомок. Потомками узла А (корня) являются все остальные узлы.

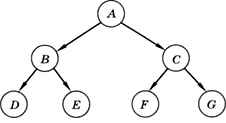
Рис. 1.12

Типичный пример иерархии — различные классификации (животных, растений, минералов, химических соединений). Например, отряд Хищные делится на два подотряда: Псообразные и Кошкообразные. В каждом из них выделяют несколько семейств (рис. 1.13).

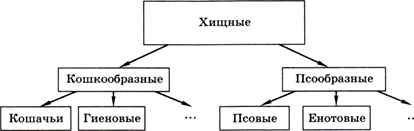
Рис. 1.13

Конечно, на рис. 1.13 показаны не все семейства, остальные обозначены многоточиями.

В текстах иерархию часто представляют в виде многоуровневого списка. Например, оглавление книги о хищниках может выглядеть так:

Работая с файлами и папками, мы тоже встречаемся с иерархией: классическая файловая система имеет древовидную структуру ¹. Вход в папку — это переход на следующий (более низкий) уровень иерархии (рис. 1.14).

---

¹ В современных файловых системах (NTFS, ext3) файл может «принад¬лежать» нескольким каталогам одновременно. При этом древовидная структура, строго говоря, нарушается.

---

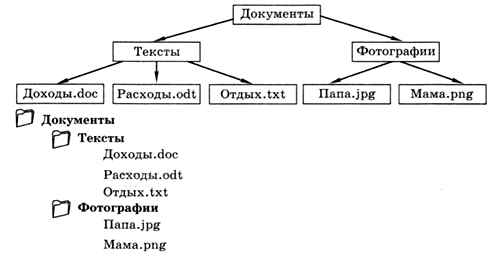
Рис. 1.14

Алгоритм вычисления арифметического выражения тоже может быть представлен в виде дерева (рис. 1.15).

(а + 3) * 5 - 2 * b

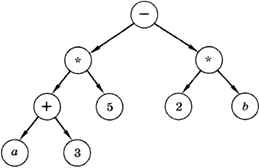
Рис. 1.15

Здесь листья — это числа и переменные, тогда как корень и промежуточные вершины — знаки операций. Вычисления идут «снизу вверх», от листьев — к корню. Показанное дерево можно записать так:

(-(*(+ (а,3),5),*(2,b)))

Самое интересное, что скобки здесь необязательны; если их убрать, то выражение всё равно может быть однозначно вычислено:

* + а35 * 2b

Такая запись, которая называется префиксной (операция записывается перед данными), просматривается с конца. Как только встретится знак операции, эта операция выполняется с двумя значениями, записанными справа. В рассмотренном выражении сначала выполняется умножение:

- * + а 3 5 (2*b)

затем — сложение:

- * (а + 3) 5 (2 * b)

и ещё одно умножение:

- (а + 3) * 5 (2*b)

и наконец, вычитание:

(а + 3) * 5 - (2 * b)

Для получения префиксной записи мы обходили все узлы дерева в порядке «корень — левое поддерево — правое поддерево». Действительно, сначала записана метка корня («-»), затем все метки левого поддерева, а затем — все метки правого поддерева. Для поддеревьев используется тот же порядок обхода. Если же обойти дерево в порядке «левое поддерево — правое поддерево — корень», получается постфиксная форма (операция после данных). Например, рассмотренное выше выражение может быть записано в виде

аЗ+5*2b*-

Для вычисления такого выражения скобки также не нужны, и это очень удобно для автоматических расчётов. Когда программа на языке программирования высокого уровня переводится в машинные коды, часто все выражения записываются в бесскобочной постфиксной форме и именно так и вычисляются. Постфиксная форма для компьютера удобнее, чем префиксная, потому что, когда программа доходит до знака операции, все данные для выполнения этой операции уже готовы.

Следующая страница Графы

Cкачать материалы урока