Урок 4
Структура информации (простые структуры). Деревья. Графы
§4. Структура информации
Содержание урока
Зачем структурировать информацию?
Графы
Практическая работа № 1 «Оформление документа»
Практическая работа № 2 «Структуризация информации (таблица, списки)»
Практическая работа № 3 «Структуризация информации (деревья)»
Практическая работа № 4 «Графы»
Графы
Подумайте, как можно структурировать такую информацию:
«От посёлка Васюки три дороги идут в посёлки Солнцево, Грибное и Ягодное. Между Солнцевым и Грибным и между Грибным и Ягодным также есть дороги. Кроме того, есть дорога, которая идет из Грибного в лес и возвращается обратно в Грибное».
Можно, например, нарисовать схему дорог (рис. 1.16, а). На рисунке 1.16, б населённые пункты для краткости обозначены латинскими буквами.
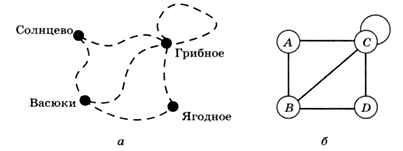
Рис. 1.16
Для исследования таких схем используют графы.
Граф — это набор вершин и связей между ними (рёбер).
Для хранения информации о вершинах и связях графа, соответствующего схеме на рис. 1.16, можно использовать таблицу (матрицу), показанную на рис. 1.17.
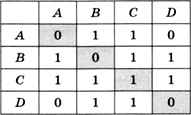
Рис. 1.17
Единица на пересечении строки А и столбца В означает, что между вершинами А и В есть связь. Ноль указывает на то, что связи нет. Такая таблица называется матрицей смежности. Она симметрична относительно главной диагонали (серые клетки в таблице).
На пересечении строки С и столбца С стоит единица, которая говорит о том, что в графе есть петля — ребро, которое начинается и заканчивается в одной и той же вершине.
Можно поступить иначе: для каждой вершины перечислить все вершины, с которыми связана данная вершина. В этом случае мы получим список смежности. Для рассмотренного графа список смежности выглядит так:
(А (В, С), В (А, С, D), С (А, В, С, В), D (В, С))
Строго говоря, граф — это математический объект, а не рисунок. Конечно, его можно нарисовать на плоскости (например, как на рис. 1.16, б), но матрица смежности и список смежности не дают никакой информации о том, как именно следует располагать узлы друг относительно друга. Для таблицы на рис. 1.17 возможны, например, варианты, показанные на рис. 1.18.
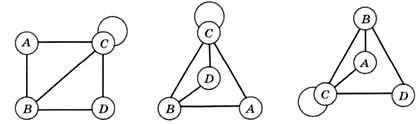
Рис. 1.18
В рассмотренном примере все вершины связаны, т. е. между любой парой вершин существует путь — последовательность рёбер, по которым можно перейти из одного узла в другой. Такой граф называется связным.
Связный граф — это граф, между любыми вершинами которого существует путь.
Теперь представьте себе, что дороги Басюки — Солнцево, Басюки — Грибное и Грибное — Ягодное завалило снегом (или размыло дождём) так, что по ним не пройти и не проехать (рис. 1.19).
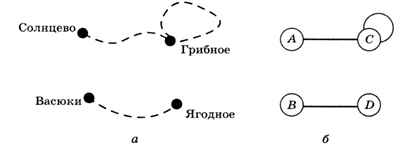
Рис. 1.19
Схему на рис. 1.19, а тоже можно считать графом (она подходит под определение), но в таком графе есть две несвязанные части, каждая из которых — связный граф. Такие части называют компонентами связности.
Вспоминая материал предыдущего пункта, можно сделать вывод, что дерево — это частный случай связного графа. Но у дерева есть одно важное свойство — в нём нет замкнутых путей (циклов). Граф на рис. 1.17 не является деревом, потому что в нём есть циклы: АВСА, BCDB, ABDCA.
Дерево — это связный граф, в котором нет циклов.
Если в первом примере с дорогами нас интересуют ещё и расстояния между поселками, каждой связи нужно сопоставить число (вес) (рис. 1.20).
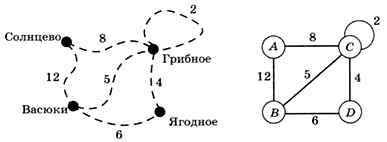
Рис. 1.20
Такой граф называется взвешенным, поскольку каждое ребро имеет свой вес. Весом может быть не только расстояние, но и, например, стоимость проезда или другая величина.
Как хранить информацию о таком графе? Ответ напрашивается сам собой — нужно в таблицу записывать не 1 или 0, а вес ребра. Если связи между двумя вершинами нет, на бумаге можно оставить ячейку таблицы пустой, а при хранении в памяти компьютера записывать в неё условный код, например -1. Такая таблица называется весовой матрицей, потому что содержит веса рёбер. В данном случае она выглядит, как показано на рис. 1.21.
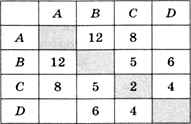
Рис. 1.21
Так же как и матрица смежности, весовая матрица симметрична относительно главной диагонали. Нижняя ячейка в столбце А и верхняя в столбце D говорят о том, что между вершинами А и D нет ребра.
Если в графе немного вершин, весовая матрица позволяет легко определить наилучший маршрут из одной вершины в другую простым перебором вариантов. Рассмотрим граф, заданный весовой матрицей на рис. 1.22 (числа определяют стоимость поездки между соседними пунктами).
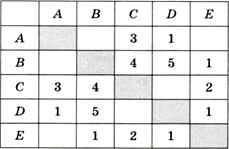
Рис. 1.22
Найдём наилучший путь из А в В — такой, при котором общая стоимость поездки минимальная. Сначала видим, что из пункта А напрямую в В ехать нельзя, а можно ехать только в С и D. Изобразим это на схеме (рис. 1.23).
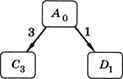
Рис. 1.23
Числа около рёбер показывают стоимость поездки по этому участку, а индексы у названий вершин показывают общую стоимость проезда в данную вершину из вершины А.
Теперь разберём варианты дальнейшего движения из вершины С (вершину А уже не нужно рассматривать, так как мы из неё пришли) (рис. 1.24).
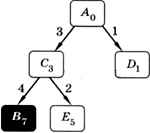
Рис. 1.24
Видим, что из С сразу можно попасть в В, стоимость проезда в этом случае равна 7. Но, возможно, это не самый лучший вариант, и нужно проверить ещё путь через вершину Е. Действительно, оказывается, что можно сократить стоимость до 6 (рис. 1.25).
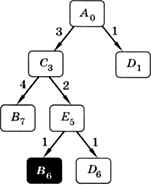
Рис. 1.25
Исследовать дальше маршрут, содержащий цепочку ACED, нет смысла, потому что его стоимость явно будет больше 6. Аналогично строим вторую часть схемы (вы догадались, что схема представляет собой дерево!) (рис. 1.26).
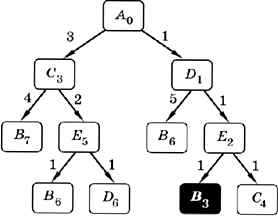
Рис. 1.26
Таким образом, оптимальный (наилучший) маршрут — ADEB, его стоимость — 3. Маршрут ADEC, не дошедший до вершины В, далее проверять не нужно, он не улучшит результат.
Конечно, для более сложных графов метод перебора работает очень долго, поэтому используются более совершенные (но более сложные) методы, о которых мы поговорим в 11 классе.
Наверное, вы заметили, что при изображении деревьев, которые описывают иерархию (подчинение), мы ставили стрелки от верхних уровней к нижним. Это означает, что для каждого ребра указывается направление, и двигаться можно только по стрелкам, но не наоборот. Такой граф называется ориентированным (или коротко орграфом). Он может служить, например, моделью системы дорог с односторонним движением. Матрица смежности и весовая матрица для орграфа уже не обязательно будут симметричными.
На схеме на рис. 1.27 всего две дороги с двусторонним движением, по остальным можно ехать только в одну сторону.
Рёбра в орграфе называют дугами. Дуга, в отличие от ребра, имеет начало и конец.
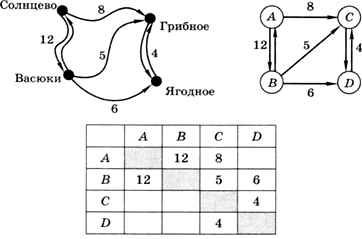
Рис. 1.27
Рассмотрим следующую задачу: определить количество возможных путей из вершины А в вершину К для ориентированного графа, показанного на рис. 1.28.
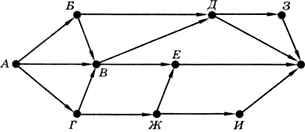
Рис. 1.28
Так как граф ориентированный, переходить в другую вершину можно только по стрелкам. Будем двигаться по стрелкам от начальной вершины А. Около каждой вершины запишем количество возможных путей из вершины А в эту вершину. Найдём все вершины, в которые можно попасть только из А: это вершины Б и Г, записываем около них количество путей 1 (рис. 1.29).
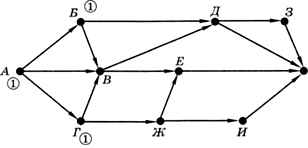
Рис. 1.29
Теперь ищем вершины, в которые можно попасть только из уже отмеченных вершин. Например, в вершину В есть один путь из А напрямую, а также по одному пути через Б и Г (так как эти вершины отмечены числом 1). Общее количество путей из А в В вычисляется как сумма отметок предыдущих вершин. В данном случае получаем всего три маршрута из А в В. В вершину Ж можно попасть только из Г, поэтому число путей в Г и Ж совпадает (рис. 1.30).
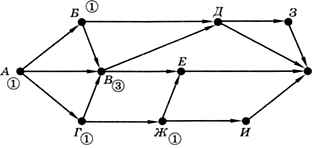
Рис. 1.30
В вершину Д идёт один путь через В и три пути через В, поэтому общее число путей — четыре. Аналогично получаем четыре пути в вершину Е: три пути через В и один — через Ж (рис. 1.31).
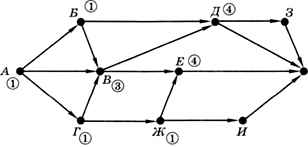
Рис. 1.31
Далее находим один путь из А в If (только через Ж) и четыре пути из А в 3 (все через Д). В конечную вершину К можно попасть через вершины Д (четыре пути), 3 (четыре пути), Е (четыре пути) и И (один путь), таким образом, общее количество различных путей равно 13 (рис. 1.32).
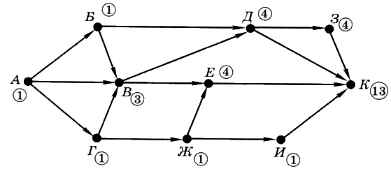
Рис. 1.32
Следующая страница 
Вопросы и задания
Cкачать материалы урока
