Уроки 10 - 11
Восьмеричная и шестнадцатеричная системы счисления
§12. Восьмеричная система счисления. §13. Шестнадцатеричная система счисления
Содержание урока
§12. Восьмеричная система счисления
Восьмеричная система
Алгоритм перевода восьмеричного числа в двоичную систему счисления
Алгоритм перевода двоичного числа в восьмеричную систему счисления
§13. Шестнадцатеричная система счисления
§12. Восьмеричная система счисления
Восьмеричная система
Восьмеричная система счисления (система с основанием 8) использовалась для кодирования команд во многих компьютерах 1950-1980-х гг. (например, в американской серии PDP-11, советских компьютерах серий ДВК, СМ ЭВМ, БЭСМ). В ней используются цифры от 0 до 7.
Для перевода десятичного числа в восьмеричную систему проще всего использовать стандартный алгоритм для позиционных систем (деление на 8, выписывание остатков в обратном порядке). Например:
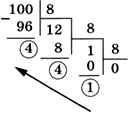
Для перевода из восьмеричной системы в десятичную значение каждой цифры умножают на 8 в степени, равной разряду этой цифры, и полученные произведения складывают:
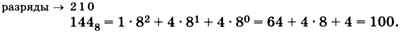
Более интересен перевод из восьмеричной системы в двоичную и обратно. Конечно, можно перевести число сначала в десятичную систему, а потом — в двоичную. Но для этого требуется выполнить две непростые операции, в каждой из них легко ошибиться.
Оказывается, можно сделать перевод из восьмеричной системы в двоичную напрямую, используя тесную связь между этими системами: их основания связаны равенством 23 = 8.
Покажем это на примере восьмеричного числа 7538. Запишем его в развёрнутой форме:
7538 = 7 • 82 + 5 • 81 + 3 • 80 - 7 • 26 + 5 • 23 + 3 • 20.
Теперь переведём отдельно каждую цифру в двоичную систему:
7 = 1112 = 1 • 22 + 1 • 21 + 1 • 20,
5 = 1012 = 1 • 22 + 1 • 20,
3 = 112 = 1 • 21 + 1 • 20.
Подставим эти выражения в предыдущее равенство:
7538 = (1 • 22 + 1 • 21 + 1 • 20) • 26 + (1 • 22 + 1 • 20) • 23 + (1 • 21 + 1 • 20) • 20.
Раскрывая скобки, мы получим разложение исходного числа по степеням двойки, т. е. его запись в двоичной системе счисления (здесь добавлены нулевые слагаемые для отсутствующих степеней числа 2):
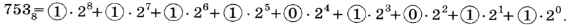
Таким образом, 7538 = 111 101 0112. Двоичная запись разбита на триады (группы из трёх цифр), каждая триада — это двоичная запись одной цифры исходного восьмеричного числа.
Следующая страница  Алгоритм перевода восьмеричного числа в двоичную систему счисления
Алгоритм перевода восьмеричного числа в двоичную систему счисления

