Урок 19
Упрощение логических выражений
§21. Упрощение логических выражений

Содержание урока

Законы алгебры логики

Логические уравнения

Задачи

Логические уравнения

Если приравнять два логических выражения, мы получим уравнение. Его решением будут значения переменных, при которых уравнение превращается в истинное равенство, т. е. когда значения левой и правой частей совпадают. Например, уравнение А • В = 1 имеет единственное решение: А = В = 1, для остальных комбинаций значений переменных левая часть равна нулю. В то же время уравнение А + В = 1 имеет три решения: (А = 0, В = 1), (А = 1, В = 0) и А = В = 1.

Пример 1. Требуется найти все решения уравнения

((B + C • А) → (А • C + D) = 0.

Вспоминаем, что импликация равна нулю только тогда, когда первое выражение равно 1, а второе — 0. Поэтому исходное уравнение сразу разбивается на два:

(B + C) • А = 1,       А • C + D = 0.

Первое уравнение с помощью закона де Моргана можно преобразовать к виду В • C • А = 1, откуда сразу следует, что все три сомножителя должны быть равны 1. Это значит, что А = 1, В = 0 и С = 0. Кроме того, из второго уравнения следует, что В=0. А=1 и С = 0 удовлетворяют и второму уравнению тоже. Решение найдено, причём оно единственное.

Возможен второй вариант — упростить выражение. Заменяя импликацию по формуле А → В = А + В получаем:

(B + C) • A + А • C + D = 0.

Используем закон де Моргана:

B + C + А + А • C + D = 0.

и закон поглощения:

В + С + А + D =0.

Для того чтобы логическая сумма была равна нулю, каждое слагаемое должно быть равно нулю, поэтому А = 1, В = С = D = 0.

Есть и третий вариант — построить таблицу истинности выражения в левой части и найти все варианты, при которых оно равно 0. Однако таблица истинности выражения с четырьмя переменными содержит 2⁴ = 16 строк, поэтому такой подход достаточно трудоёмок.

Пример 2. Требуется найти все решения уравнения

(А + В) → (В • С • D) = 1.

Преобразуем выражение, раскрыв импликацию через операции «НЕ» и «ИЛИ» и применив закон де Моргана:

А + В + В • С • D = А • В + В • С • D= 1.

Если логическая сумма равна 1, то хотя бы одно слагаемое равно 1 (или оба одновременно).

Равенство А • В = 1 верно при А = 0, В = 1 и любых С и В. Поскольку есть всего 4 комбинации значений С и D, уравнение А • В = 1 имеет 4 решения:

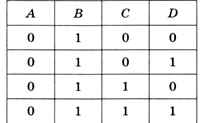
Второе уравнение, B • C • D=1, даёт В = С = D = 1 при любом А, т. е. оно имеет два решения:

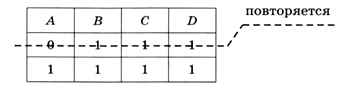
Видим, что первое из этих решений уже было получено раньше, поэтому уравнение имеет всего пять разных решений. Заметим, чтс^определить все повторяющиеся решения можно из уравнения (А • В) • (B • C • D) = 1, которое имеет единственное решение А = 0, В = С = D = 1.

Пример 3. Требуется найти число решений уравнения

A • B • C + B • C • D = 0..

Здесь, в отличие от предыдущих задач, не нужно находить сами решения, интересует только их количество. Уравнение распадается на два:

A • B • C = 0       и       B • C • D = 0.

Каждое из них имеет достаточно много решений. Можно поступить следующим образом: сначала найти количество решений «обратного» уравнения, с единицей в правой части:

A • B • C + B • C • D = 1

и затем вычесть его из 16 (общего количества комбинаций четырёх переменных). Уравнение А • В • С = 1 имеет два решения: А = В = С = 1 и любое D (0 или 1). Второе уравнение, B • C • D = 1, тоже имеет два решения: А — любое, В = С = О, D = 1. Среди этих четырёх решений нет повторяющихся, поэтому исходное уравнение имеет 16 - 4 — 12 решений.

Пример 4. Требуется найти число решений уравнения

(Х₁ → Х₂) • (Х₂ → Х₃) • (Х₃ → Х₄) • (Х₄ → Х₅) • (Х₅ → Х₆) = 1.

Так как каждая логическая переменная может принимать только значения 0 и 1, можно представить решение в виде 6-битной цепочки. Например, цепочка 010110 означает, что Х₁ = Х₃ = Х₆ = 0 и Х₂ = Х₄ = Х₅ = 1.

Заметим, что импликация А → В ложна тогда и только тогда, когда А = 1 и В = 0. Поэтому в решении заданного уравнения не может встречаться последовательность 10, иначе какая-то импликация оказывается ложной и всё выражение будет равно 0. Поэтому существует всего 7 решений:

000000 000001 000011 000111 001111 011111 111111.

Обратите внимание, что число решений логических уравнений, в отличие от «обычных уравнений», всегда конечно. Это связано с тем, что каждая переменная может принимать только два значения (0 и 1), и число разных комбинаций значений переменных конечно, оно равно 2ⁿ, где n — это количество переменных. Поэтому уравнение с n переменными имеет не более 2ⁿ решений.

Подготовьте сообщение

а) «Законы логики и правила алгебры: сходство и различия»
б) «Методы решения логических уравнений»
в) «Системы логических уравнений»

Следующая страница Задачи

Cкачать материалы урока