Урок 45
Рекурсия
§61. Рекурсия

Содержание урока

Что такое рекурсия?

Ханойские башни

Примеры

Как работает рекурсия

Вопросы и задания

Задачи

Что такое рекурсия?

Вспомним определение натуральных чисел. Оно состоит из двух частей:

1) 1 — натуральное число;

2) если n — натуральное число, то n + 1 — тоже натуральное число.

Вторая часть этого определения в математике называется индуктивной: натуральное число определяется через другое натуральное число, и таким образом определяется всё множество натуральных чисел. В программировании этот приём называют рекурсией.

Рекурсия — это способ определения множества объектов через само это множество на основе заданных простых базовых случаев.

Первая часть в определении натуральных чисел — это и есть тот самый базовый случай. Если убрать первую часть из определения, оно будет неполно: вторая часть даёт только метод перехода к следующему значению, но не даёт никакой «зацепки», не отвечает на вопрос «откуда начать». Похожим образом задаются числа Фибоначчи: первые два числа равны 1, а каждое из следующих чисел равно сумме двух предыдущих:

1) F₁ = F₂ = 1;

2) F_n = F_n-1 + F_n-2 для n > 2.

Популярные примеры рекурсивных объектов — фракталы. Так в математике называют геометрические фигуры, обладающие самоподобием. Это значит, что они составлены из фигур меньшего размера, каждая из которых подобна целой фигуре. На рисунке 8.2 показан треугольник Серпинского — один из первых фракталов, который предложил в 1915 г. польский математик В. Серпинский.

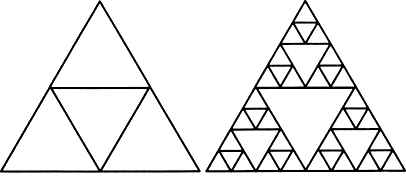
Рис. 8.2

Равносторонний треугольник делится на 4 равных треугольника меньшего размера (см. рис. 8.2, слева), затем каждый из полученных треугольников, кроме центрального, снова делится на 4 ещё более мелких треугольника и т. д. На рисунке 8.2 справа показан треугольник Серпинского с тремя уровнями деления.

Следующая страница Ханойские башни

Cкачать материалы урока