Урок 45
Рекурсия
§61. Рекурсия
Содержание урока
Ханойские башни
Ханойские башни
Согласно легенде, конец света наступит тогда, когда монахи Великого храма города Бенарас смогут переложить 64 диска разного диаметра с одного стержня на другой. Вначале все диски на низаны на первый стержень. За один раз можно перекладывать только один диск, причём разрешается класть только меньший диск на больший. Есть также и третий стержень, который можно использовать в качестве вспомогательного (рис. 8.3).
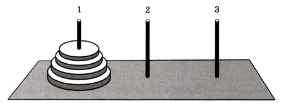
Рис. 8.3
Решить задачу для 2, 3 и даже 4 дисков довольно просто. Проблема в том, чтобы составить алгоритм для любого числа дисков.
Пусть нужно перенести п дисков со стержня 1 на стержень 3. Представим себе, что мы как-то смогли переместить п - 1 дисков на вспомогательный стержень 2. Тогда остаётся перенести самый большой диск на стержень 3, а затем п - 1 меньших дисков со вспомогательного стержня 2 на стержень 3, и задача будет решена. Получается такой псевдокод:
перенести (n-1, 1, 2)
1 -> 3
перенести (n-1, 2, 3)
Процедура перенести (которую нам предстоит написать) принимает три параметра: число дисков, начальный и конечный стержни. Таким образом, мы свели задачу переноса п дисков к двум задача переноса п - 1 дисков и одному элементарному действию — переносу 1 диска. Заметим, что при известных номерах начального и конечного стержней легко рассчитать номер вспомогательного, так как сумма номеров равна 1 + 2 + 3 = 6. Получается такая (пока не совсем верная)процедура:

Эта процедура вызывает сама себя, но с другими значениями параметров. Такая процедура называется рекурсивной.
 Рекурсивная процедура (функция) — это процедура (функция), которая вызывает сама себя напрямую или через другие процедуры и функции.
Рекурсивная процедура (функция) — это процедура (функция), которая вызывает сама себя напрямую или через другие процедуры и функции.
Основная программа для решения задачи, например, с четырьмя дисками будет содержать всего одну строку (перенести 4 диска со стержня 1 на стержень 3):
Hanoi (4, 1, 3)
Если вы попробуете запустить эту программу, она зациклится, т. е. будет работать бесконечно долго. В чём же дело? Вспомните, что определение рекурсивного объекта состоит из двух частей. В первой части определяются базовые объекты (например, первое натуральное число), именно эта часть «отвечает» за остановку рекурсии в программе. Пока мы не определили такое условие останова, процедура будет бесконечно вызывать саму себя (это можно проверить, выполняя программу по шагам). Когда же остановить рекурсию?
Очевидно, что если нужно переложить 0 дисков, задача уже решена, ничего перекладывать не надо. Это и есть условие окончания рекурсии: если значение параметра п, переданное процедуре, равно 0, нужно выйти из процедуры без каких-либо действий. Для этого в школьном алгоритмическом языке используется оператор выход (в Паскале — оператор exit). Правильная версия процедуры выглядит так:

Чтобы переложить N дисков, нужно выполнить 2N - 1 перекладываний. Для N = 64 это число равно 18 446 744 073 709 551 615. Если бы монахи, работая день и ночь, каждую секунду перемещали один диск, им бы потребовалось 580 миллиардов лет.
Следующая страница  Примеры
Примеры

