Урок 60
Оптимизация с помощью табличных процессоров
§72. Оптимизация
Содержание урока
Локальные и глобальный минимумы
Метод дихотомии
Пример: оптимальная раскройка листа
Использование табличных процессоров
Метод дихотомии
Дихотомия (греч. — деление надвое) — это метод поиска минимума функции, который очень напоминает метод деления отрезка пополам (бисекции). Пусть дана непрерывная функция f(x), имеющая на отрезке [а, b] один минимум в точке х*. Нужно найти это значение с заданной точностью ε.
Как и в методе бисекции, мы последовательно «сжимаем» отрезок, пока его ширина не будет достаточно мала (меньше, чем 2ε). На каждом шаге (рис. 9.20):
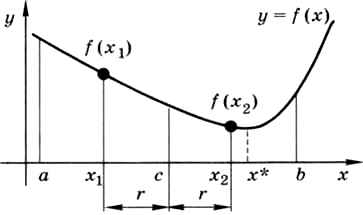
Рис. 9.20
1) вычисляется середина отрезка
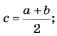
2) вычисляются координаты двух точек, симметричных относительно середины: х1 = с - r и х2 = с + r, где 0 < r < (b - а)/2 — некоторое число;
3) сравниваются значения функции в этих точках: если f(x1) > f(x2), то минимум функции находится на отрезке [х1, b], поэтому отрезок [а, х1] можно отбросить — переместить левую границу в точку х1; если f(x1) < f(x2), то правая граница отрезка перемещается в точку х2.
Остаётся один вопрос: как выбирать r на каждом шаге? Проще всего вычислять его по формуле r = k(b-a), где k — постоянный коэффициент (0 < k < 0,5). Тогда ширина отрезка на следующем шаге будет равна
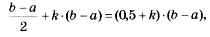
т. е. составит 0,5 + k от первоначальной ширины. Для ускорения поиска выгодно, чтобы это отношение было как можно меньше, т. е. чтобы коэффициент k был возможно ближе к нулю (ноль выбирать нельзя, потому что при этом точки х1 и х2 совпадут, и метод не будет работать). Программа может выглядеть примерно так:

В качестве упражнения можно исследовать работу этой программы при разных значениях k, подсчитав для каждого варианта количество шагов цикла, которое потребуется для получения решения с заданной точностью.
Существует вариант метода дихотомии, при котором на каждом шаге цикла нужно вычислять только одно значение функции (второе «переходит» с предыдущего шага). В этом случае нужно выбирать коэффициент k так, чтобы выполнялось равенство 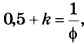 где
где 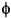 — отношение «золотого сечения»:
— отношение «золотого сечения»:
Следующая страница  Пример: оптимальная раскройка листа
Пример: оптимальная раскройка листа

