Урок 60
Оптимизация с помощью табличных процессоров
§72. Оптимизация
Содержание урока
Локальные и глобальный минимумы
Пример: оптимальная раскройка листа
Использование табличных процессоров
Пример: оптимальная раскройка листа
Рассмотрим пример практической задачи оптимизации. В углах квадратного листа железа, сторона которого равна 1 м, вырезают четыре квадрата со стороной х. Затем складывают получившуюся развёртку (по штриховым линиям на рис. 9.21), сваривают швы и таким образом получается бак.
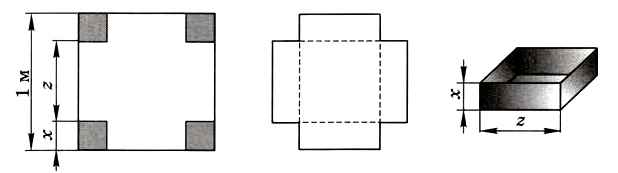
Рис. 9.21
Требуется выбрать размер выреза х так, чтобы получился бак наибольшего объёма.
Для того чтобы грамотно поставить задачу оптимизации, нужно:
1) определить целевую функцию: в данном случае выразить объём бака через неизвестную величину х;
2) задать ограничения на возможные значения х.
Легко видеть, что основание получившегося бака — это квадрат со стороной z (см. рис. 9.21), а его высота равна х. Величина z зависит от х и равна z = 1 - 2х, поэтому объём бака вычисляется по формуле V = х(1 -2х)2, это и есть целевая функция, для которой нужно найти максимум.
Понятно, что х не может быть меньше нуля. Вместе с тем х не может быть больше, чем половина стороны исходного листа (0,5 м), поэтому ограничения запишутся в виде двойного неравенства: 0 ≤ х ≤ 0,5. Заметим, что при х = 0 и х = 0,5 объём бака равен нулю (в первом случае равна нулю высота, во втором — площадь основания).
Таким образом, нужно искать максимум целевой функции f(x) = x(l -2х)2 на отрезке [0, 0,5]. Для этого можно использовать метод дихотомии (сделайте это самостоятельно). Не забудьте, что приведённый выше вариант программы рассчитан на поиск минимума, а в этой задаче нужно найти максимум.
Следующая страница 
Использование табличных процессоров
Cкачать материалы урока
