Урок 5
§5. Передача и хранение информации

Объём переданной информации

Объём переданной информации I вычисляется по формуле:

I = v • t,

где v — скорость передачи информации (в битах в секунду), a t — время передачи.

Рассмотрим несколько примеров решения задач, имеющих отношение к процессу передачи информации.

Для более наглядного представления условий некоторых задач, связанных с процессами передачи информации, удобно рисовать диаграмму, изображающую два и более процесса с разметкой временных отметок их начал и окончаний. Примером такой диаграммы является диаграмма Гантта.

Диаграмма Гантта представляет собой размещённые вдоль горизонтальной шкалы времени отрезки (прямоугольные полоски), каждый из которых соответствует отдельному процессу или задаче. Начало, конец и длина каждого такого отрезка соответствуют началу, концу и длительности того или иного процесса, а сами отрезки располагаются друг под другом со сдвигом по горизонтали.

Для наглядного представления последовательности реализации (синхронизации) нескольких процессов можно использовать диаграммы процессов или диаграммы Гантта.

Пример 1. У Толи есть доступ к сети Интернет по высокоскоростному одностороннему радиоканалу, обеспечивающему скорость получения информации 2²⁰ бит/с. У Миши нет скоростного доступа в Интернет, но есть возможность получать информацию от Толи по низкоскоростному телефонному каналу со средней скоростью 2¹³ бит/с. Миша договорился с Толей, что тот будет скачивать для него данные объёмом 5 Мбайт по высокоскоростному каналу и ретранслировать их Мише по низкоскоростному каналу. Компьютер Толи может начать ретрансляцию данных не раньше, чем им будут получены первые 0,5 Мбайт этих данных.

Каков минимально возможный промежуток времени (в секундах) с момента завершения скачивания данных Толей до полного их получения Мишей?

Как скоро Миша сможет полностью получить все данные, если Толя начнёт их скачивание в 16:00?

В этой задаче мы имеем дело с двумя процессами передачи информации, осуществляемыми с разной скоростью.

1. Процесс скачивания информации Толей по высокоскоростному каналу. Длительность этого процесса 5 • 2²³/2²⁰ = 5 • 2³ = 40 с.

2. Процесс скачивания информации Мишей по низкоскоростному каналу. Длительность этого процесса 5 • 2²³/2¹³ = 5 • 2¹⁰ = 5120 с.

При решении задач необходимо согласовывать размерности величин.

Так, если скорость передачи информации задана в битах в секунду, то и значения объёмов информации следует выразить в битах.

Из условия задачи следует, что второй процесс начинается спустя некоторое время после начала первого процесса. Вычислим это время:

0,5 • 2²³/2²⁰ = 0,5 • 2³ = 4 с.

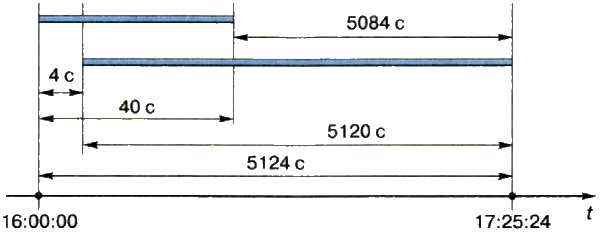
На диаграмме Гантта результаты проведённых расчётов можно изобразить так:

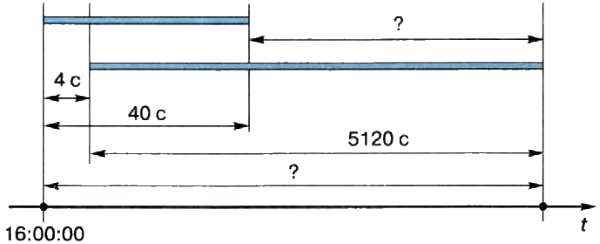
На диаграмме видно, что для ответа на первый вопрос надо найти разность:

5120 - (40 - 4) = 5120 - 36 = 5084 с.

Ответ на второй вопрос получим, выполнив следующие вычисления:

5120 + 4 = 5124 с,

5124 с = 85 мин 24 с = 1 ч 25 мин 24 с.

Полностью получить все данные Миша сможет не ранее чем в 17:25:24.

Диаграмму Гантта можно дополнить полученными результатами:

Cкачать материалы урока