Урок 26
§21. Элементы схемотехники. Логические схемы

21.2. Сумматор

Из отдельных логических элементов можно составить устройства, производящие арифметические операции над двоичными числами.

Электронная логическая схема, выполняющая суммирование двоичных чисел, называется сумматором.

Вспомним схему сложения двух n-разрядных двоичных чисел (рис. 4.9).

Рис. 4.9. Схема сложения двух n-разрядных двоичных чисел

Заметим, что при сложении цифр в i-м разряде мы должны сложить цифру a_i числа а, цифру b_i числа b, а также р_i — перенос из (i - 1)-го разряда. В результате сложения должны получиться цифра результата s_i и цифра переноса (0 или 1) в следующий разряд p_i+1.

Основываясь на этих рассуждениях, построим таблицу истинности для функций, которые в зависимости от цифр a_i, b_i и p_i получают цифры s_i и p_i+l.

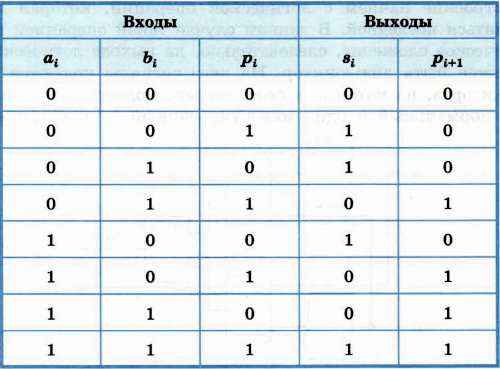
Вам известен алгоритм построения логического выражения по таблице истинности. Воспользуемся им и запишем выражение для функции p_i+1:

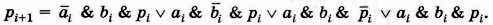
Попытаемся упростить это выражение, воспользовавшись тем, что A v А = А. Основываясь на этом законе, включим в имеющуюся дизъюнкцию ещё два слагаемых вида a_i & b_i & p_i, причём на основании коммутативного и ассоциативного законов преобразуем полученное выражение к виду:

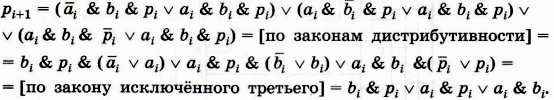
Полученное выражение означает, что функция р_i+1 принимает значение 1 только для таких комбинаций входных переменных, когда хотя бы две переменные имеют единичные значения. Обратите внимание на то, что такой вывод можно сделать и в результате анализа таблицы истинности.

По таблице истинности можем записать выражение для s_i:

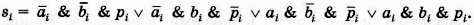
Его также можно попытаться преобразовать к более короткому виду. Но можно пойти другим путём и провести более тщательный анализ таблицы истинности для функции s_i.

Из таблицы видно, что значение s_i равно 1, если все входные сигналы равны 1. Этому соответствует выражение a_i & b_i & p_i = 1.

Или значение s_i равно 1, если в комбинации входных сигналов есть единственная 1, т. е. единица среди переменных есть, но нет одновременно двух переменных, значения которых равны

1. Это можно записать так:

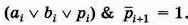
Следовательно, s,- можно записать так:

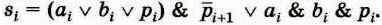
Можно попытаться самостоятельно провести преобразование логического выражения, полученного по таблице истинности для s_i к итоговому виду. Но, чтобы убедиться в равносильности этих двух выражений, достаточно построить таблицу истинности для второго из них.

Полученные выражения позволяют реализовать одноразрядный двоичный сумматор схемой, представленной на рисунке 4.10.

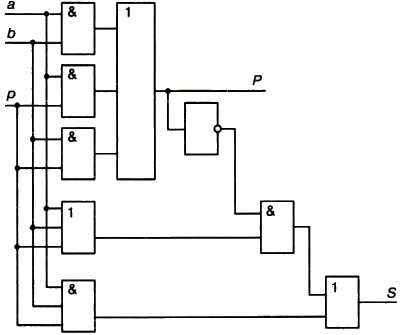
Рис. 4.10. Схема одноразрядного сумматора

Выразить s_i и p_i+1 можно и другими формулами. Например, самое короткое выражение для s_i имеет вид: s_i = a_i ⊕ b_i ⊕ p_i, что позволяет построить сумматор, используя другие логические элементы.

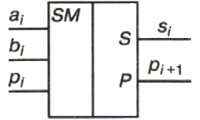
Сложение n-разрядных двоичных чисел осуществляется с помощью комбинации одноразрядных сумматоров (условное обозначение одноразрядных сумматоров приведено на рисунке слева).

Cкачать материалы урока