Уроки 3 - 4
§1.3. Передача информации. Практическая работа 1.1. Шифрование и дешифрование
Передача информации
Содержание урока
1.3.1. Сигнал. Кодирование и декодирование
1.3.2. Равномерные и неравномерные коды. Условие Фано
1.3.4. Скорость передачи информации
Практическая работа 1.1. Шифрование и дешифрование
1.3.2. Равномерные и неравномерные коды. Условие Фано
Кодирование информации может быть произведено так, что каждый получаемый код имеет одну и ту же длину. Например, французский инженер и изобретатель Эмиль Бодо в 1870 году разработал для своего телеграфа особый код — код Бодо (рис. 1.11), в котором каждая буква, цифра или другой знак кодировался при помощи комбинации из пяти сигналов. Такая телеграфная система могла, например, передавать информацию по пяти параллельным электрическим линиям, когда тот или иной символ кодировался наличием или отсутствием электрического тока в той или иной из этих пяти линий.
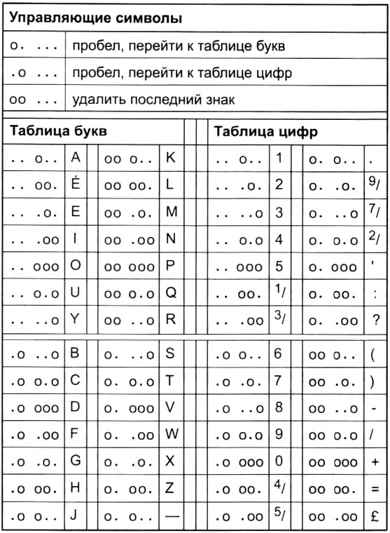
Рис. 1.11
Очевидно, что каждому символу соответствует код одной и той же длины, а суммарный размер закодированной текстовой строки может быть вычислен умножением количества символов на длину одного кода. Такой код называют равномерным кодом, или кодом постоянной длины, а кодирование, соответственно, называют равномерным кодированием.
Равномерное кодирование реализовать достаточно просто. Но такой способ кодирования не всегда оптимален. Вспомним, что различные буквы и другие символы встречаются в тексте с разной частотой. Так, в текстах на русском языке буквы «А», «О», «И» встречаются гораздо чаще, чем, например буква «Ы» или «Ъ». При кодировании такого текста более выгодно назначать буквам коды различной длины в зависимости от частоты встречаемости этих букв.
Для «А», «О», «И» и других часто используемых букв можно использовать более короткие коды, а для редко используемых символов — коды большей длины. Такие коды называют неравномерными, или кодами переменной длины, а кодирование — неравномерным.
Примером неравномерного кода является азбука Морзе (рис. 1.12).
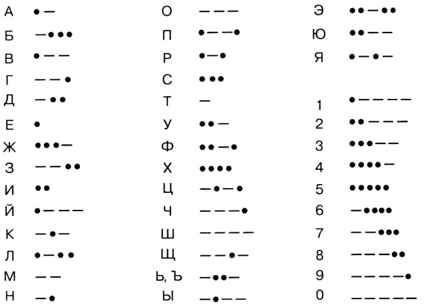
Рис. 1.12
В компьютере информация представлена в виде последовательностей нулей и единиц, поэтому в качестве кодов обычно используются последовательности именно этих цифр. Например, в азбуке Морзе можно заменить точки нулями, а тире — единицами. Тогда строка текста «КОД МОРЗЕ» может быть закодирована так — рис. 1.13.
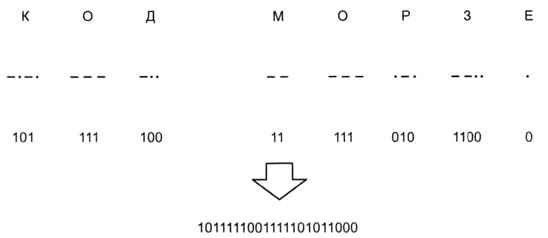
Рис. 1.13
При этом возникает вопрос: как обеспечить однозначность декодирования такого кода — так, чтобы полученную при кодировании «сплошную» последовательность нулей и единиц можно было разделить на коды, соответствующие «правильным» буквам. Для обеспечения однозначности декодирования закодированного сообщения необходимо выбирать неравномерные коды такими, что при «разборе» закодированной последовательности слева направо (или справа налево) каждый раз можно было отделять от неё очередной код единственным способом.
Правило, согласно которому необходимо формировать такой набор кодов, достаточно простое: никакой код не должен совпадать с началом никакого другого кода. Это правило называют условием Фано (в честь Роберта Фано — американского учёного - информатика итальянского происхождения).
Примеры
1. Набор кодов, соответствующий условию Фано:
2. Набор кодов, не соответствующий условию Фано:
В этом наборе кодов условие Фано нарушено для кодов, соответствующих буквам «Б» (10) и «В» (100), так как код буквы «Б» совпадает с началом кода буквы «В».
В результате, например, строка 100 может быть декодирована неоднозначно — или как одна буква «В», или как пара букв «БА».
Следующая страница 
1.3.3. Искажение информации
Cкачать материалы урока
