Уроки 50 - 51
§4.1. Алгоритм и кодирование основных алгоритмических структур
§4.1.3. Подпрограммы. Рекурсивные алгоритмы
Содержание урока
§4.1.1. Алгоритм и его свойства
§4.1.2. Алгоритмические структуры «ветвление» и «цикл»
§4.1.3. Подпрограммы. Рекурсивные алгоритмы
§4.1.4. Приёмы отладки программ. Трассировка программ
Подпрограммы. Рекурсивные алгоритмы
Подпрограммы. Во многих алгоритмах те или иные действия могут повторяться для различных исходных данных. Например, пусть нужно составить алгоритм для вычисления площади круговой пластины с круглыми отверстиями (рис. 4.5). Очевидно, для этого нужно вычислить площадь круга, соответствующего внешнему контуру пластины, и вычесть из нее сумму площадей круговых отверстий.
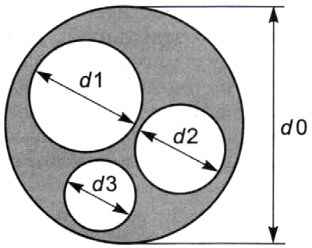
Рис. 4.5
В алгоритме для вычисления площади пластины потребуется записать четыре одинаковых вычислительных блока, в которых рассчитывается площадь круга диаметром, соответственно, d0, d1, d2, d3 (рис. 4.6).
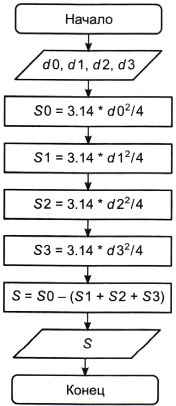
Рис. 4.6
Существует возможность упростить такой алгоритм, вынеся из него однотипные действия в отдельный, подчинённый алгоритм и обращаясь к подчинённому алгоритму из основного (главного) алгоритма с требуемыми исходными данными (рис. 4.7). Такой подчинённый алгоритм реализуется в виде подпрограммы. Когда подпрограмма завершает работу, происходит возврат из неё в основную программу, которой передаются результаты работы подпрограммы.
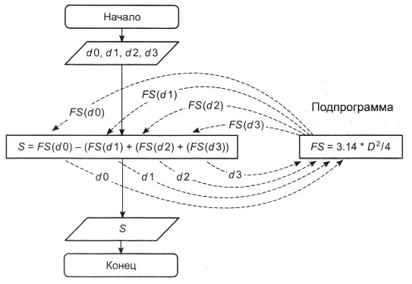
Рис. 4.7
Процедуры и функции. Возможны два вида подпрограмм, различающиеся принципами их вызова и количеством возвращаемых ими значений.
Функция — это подпрограмма, которая, принимая одно или несколько исходных данных, возвращает единственное значение, являющееся результатом работы этой функции. Такая подпрограмма аналогична математическим функциям (например, тригонометрическим, которые по заданному значению угла вычисляют его синус, косинус, тангенс и т. д.). Обращение к функции (вызов функции) обычно записывается так же, как это делается в математике, например:
X = SIN (А) — вызов функции, вычисляющей значение синуса угла, величина которого задана в переменной А; результат, возвращенный этой функцией, записывается в переменную X;
Y = SQRT (1 - COS (A) *COS (A)) — реализация вычисления значения синуса угла по формуле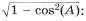 
здесь результаты, возвращаемые функциями вычисления косинуса угла А, сразу же используются в арифметическом выражении, значение которого, в свою очередь, затем используется в качестве исходных данных для функции вычисления квадратного корня (SQRT).
Обычно при написании алгоритма подпрограммы-функции после выполнения всех вычислений полученные результаты нужно записать в специальную переменную. Именно её значение возвращается в основной алгоритм в качестве результата работы функции.
В современных языках программирования предусматривается большое количество различных готовых функций (стандартных, или библиотечных), которые достаточно вызывать из основного алгоритма. Однако при необходимости можно создавать свои собственные (пользовательские) функции, реализующие любой алгоритм.
Процедура — подпрограмма, которая может принимать любое количество исходных данных и возвращать любое количество значений в качестве результатов своей работы. Обращение к процедуре в основном алгоритме записывается отдельной командой: и исходные данные, и переменные, в которые должны быть записаны результаты работы процедуры, записываются в скобках списком через запятую (сначала перечисляются исходные данные, а затем — переменные-результаты). Вызовы процедур не могут использоваться в арифметических выражениях (в отличие от функций).
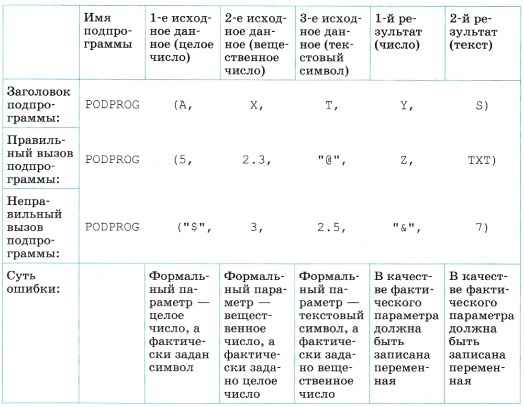
Формальные и фактические параметры. Для удобства и большей универсальности при написании подпрограмм переменные, используемые в алгоритме подпрограммы, обычно полностью независимы от переменных, используемых в основном алгоритме (даже если совпадают имена этих переменных). Принято считать, что подпрограмма использует отдельное адресное пространство. Соответственно, переменные, используемые внутри подпрограммы, называют локальными.
Чтобы обеспечить передачу данных из основного алгоритма в подпрограмму и возврат из подпрограммы результатов её работы, используется механизм формальных и фактических параметров.
• При написании подпрограммы в её заголовке записывается «шаблон» вызова этой подпрограммы. Он включает имя подпрограммы и записанный в скобках список локальных переменных, используемых внутри подпрограммы. Эти переменные представляют собой передаваемые в подпрограмму исходные {входные) данные, а для процедуры — также список локальных переменных, в которые в процедуре записываются результаты вычислений. Все эти переменные, записанные в заголовке подпрограммы, называют формальными параметрами.
• При вызове подпрограммы из основного алгоритма в строке обращения к подпрограмме записывается её имя, а в скобках — список передаваемых ей реальных исходных значений и (для процедуры) список переменных, в которые после выполнения процедуры будут записаны результаты её работы. В качестве исходных данных могут быть записаны константы, переменные, арифметические выражения или подпрограммы- функции. Все эти исходные данные и переменные для записи результатов называют фактическими параметрами.
Для правильной работы подпрограммы необходимо соблюдать правило: количество, порядок записи и типы формальных и фактических параметров должны совпадать 1.
1) Кроме особых случаев, когда часть фактических параметров может быть пропущена. Такая возможность реализуется особыми приёмами программирования. Вместо отсутствующих фактических параметров в подпрограмме тогда используются некие заранее оговоренные и занесённые в алгоритм подпрограммы значения «по умолчанию».
Например:
Процедуры — обработчики событий. Современные программы для компьютеров обычно пишутся по объектному принципу. Рассматривается некий набор объектов — как отображаемых визуально (изображаемые на экране окна, кнопки и другие элементы интерфейса), так и не имеющих визуального представления (например, аудиозапись). Каждый такой объект может иметь свой набор свойств, значения которых можно задать при создании объекта, а затем изменять при выполнении программы. Кроме того, рассматривается некоторый набор возможных событий — ситуаций, как возникающих при работе самого компьютера и его периферийных устройств (скажем, замятие бумаги в принтере), так и инициированных пользователем (например, в качестве события может выступать щелчок кнопкой мыши или нажатие определённой клавиши на клавиатуре).
Для каждого объекта и каждого возможного события, совершаемого над ним, разрабатывается отдельная процедура — алгоритм, определяющий действия компьютера при возникновении того или иного события. Такая процедура называется обработчиком события.
При отсутствии событий компьютер находится в «ждущем» режиме — не выполняет никаких действий, которые можно было бы наблюдать со стороны. Если же для какого-то объекта произойдёт то или иное событие, для которого была предусмотрена процедура-обработчик, то компьютер запустит в работу именно её. Если произойдёт несколько событий для одного и того же или для разных объектов (одновременно или поочерёдно, когда новое событие происходит до завершения обработки предыдущего), то компьютер может запустить несколько соответствующих обработчиков, — если только их выполнение не противоречит друг другу.
Рекурсивные алгоритмы. Возможна ситуация, когда в ходе выполнения подпрограммы её алгоритмом предусматривается вызов самой этой же подпрограммы. Такой приём называют рекурсией, а подобные алгоритмы с «самовызовом» называют рекурсивными алгоритмами.
Пример использования рекурсии — вычисление факториала.
Факториалом натурального числа называют значение, равное произведению этого числа на все числа натурального ряда, меньшие данного числа. Факториал обозначается восклицательным знаком, записанным после исходного числа. Например, факториал числа 4 вычисляется так: 4! = 4 • 3 • 2 • 1.
Создадим для решения этой задачи рекурсивный алгоритм в виде подпрограммы, которой в качестве исходного данного будет передаваться значение 4.
Предположим, что мы уже знаем, чему равен факториал предыдущего натурального числа. Тогда для вычисления 4! достаточно умножить это уже известное значение 3! на число 4.
Однако мы пока не знаем, чему равен 3!. Вычислить его мы можем... вызвав эту же самую подпрограмму, которую мы пишем для вычисления факториала числа 4. Но теперь в эту подпрограмму в качестве исходного данного передается число 3. И вычисление значения 3! производится по тому же принципу: число 3 умножается на 21.
Поскольку величина 2! нам тоже пока неизвестна, её мы вычислим снова вызовом этой же подпрограммы, которой будет передано уже число 2. И здесь вычисление производится тоже умножением числа 2 на факториал предыдущего числа 1 (и тоже вызовом нашей же подпрограммы с передачей ей исходного данного — числа 1).
Но вот чему равен факториал единицы, мы знаем точно: он равен единице. И этот факт можно отразить в нашей подпрограмме при помощи оператора ветвления типа: «ЕСЛИ переданное число равно 1, то результат равен 1».
Запишем теперь (на псевдокоде; это условный язык — смесь языка программирования и естественного (русского, английского) языка) соответствующую подпрограмму:
А теперь посмотрим, как работает этот алгоритм, например, для числа 4 (из основного алгоритма производится вызов подпрограммы в виде F = FAKTOR (4)). Для этого будем отслеживать изменение значения переменной N (рис. 4.8).
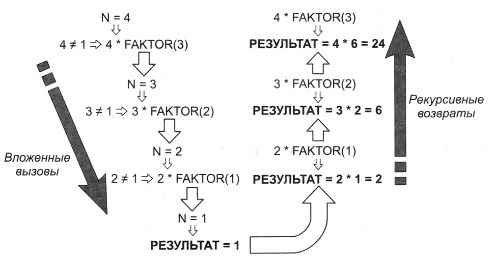
Рис. 4.8
Как видим, в процессе работы подпрограммы сначала формируется цепочка её вложенных вызовов — до тех пор, пока не сработает условие завершения рекурсии (в данном случае N = 1). После этого в каждом из выполненных вложенных вызовов — начиная с самого последнего и в обратном порядке — производится вычисление результата и возврат в предыдущий вложенный вызов подпрограммы. Такая обратная цепочка рекурсивных возвратов выполняется, пока не произойдёт возврат в самый первый вызов подпрограммы. А когда в ней будет вычислен окончательный результат, происходит возврат в основной алгоритм.
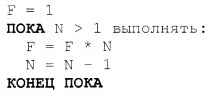
Важно помнить, что использовать рекурсию нужно оптимально. Некоторые задачи более просто и изящно решаются при помощи рекурсии. Но во многих случаях гораздо быстрее и проще разработать обычный, нерекурсивный алгоритм. Например, для вычисления факториала можно использовать обычный цикл (ниже приведен фрагмент алгоритма):
Вопросы и задания
1. Что такое подпрограмма? Для чего используются подпрограммы?
2. Сформулируйте основные различия между подпрограммой-функцией и подпрограммой-процедурой. В каких случаях предпочтительно использовать тот или иной из этих двух видов подпрограмм? Приведите примеры.
3. Что понимается под стандартными функциями? Как вы считаете, почему их называют стандартными? Найдите в Интернете информацию о том, почему такие функции называют библиотечными.
4. Как работает механизм передачи данных между основным алгоритмом и подпрограммой при помощи формальных и фактических параметров? Какое основное правило при этом должно соблюдаться?
5. Что такое обработчики событий? Чем работа таких процедур отличается от работы обычных подпрограмм-процедур?
6. Что такое рекурсия? Как работают рекурсивные алгоритмы?
*7. Приведите свой пример построения рекурсивного алгоритма. Опишите последовательность вложенных вызовов и рекурсивных возвратов при работе вашего рекурсивного алгоритма.
Следующая страница 
§4.1.4. Приёмы отладки программ. Трассировка программ
Cкачать материалы урока
