Уроки 50 - 51
§4.1. Алгоритм и кодирование основных алгоритмических структур
§4.1.5. Типовые алгоритмы
Содержание урока
§4.1.1. Алгоритм и его свойства
§4.1.2. Алгоритмические структуры «ветвление» и «цикл»
§4.1.3. Подпрограммы. Рекурсивные алгоритмы
§4.1.4. Приёмы отладки программ. Трассировка программ
§4.1.5. Типовые алгоритмы
Типовые алгоритмы
Некоторые алгоритмы используются настолько часто, что считаются типовыми. Рекомендуется знать принципы построения этих алгоритмов, их принципы работы и уметь опознавать эти алгоритмы (уметь определять по виду алгоритма, какую задачу он решает).
Алгоритм нахождения наибольшего из нескольких чисел
Задано два, три, четыре или более исходных чисел. Требуется определить (и, например, вывести на экран) максимальное из них.
Принцип решения задачи
Исходные числа при их вводе записываются в соответствующие переменные (например, а, Ь, с).
Определить наибольшее из двух чисел позволяет оператор ветвления, условие в котором сводится к сравнению этих двух чисел:
ЕСЛИ a>b ТО Мах = а ИНАЧЕ Мах = b
Если требуется найти максимальное из трёх чисел, то проще всего использовать несколько операторов ветвления с соответствующими сложными условиями 1):
ЕСЛИ (a>=b) И (a>=с) ТО Мах = а
ЕСЛИ (b>=а) И (b>=c) ТО Мах = b
ЕСЛИ (c>=а) И (c>=b) ТО Мах = с
1) В условии используется сравнение «больше или равно», чтобы обеспечить корректную работу алгоритма в случае равенства чисел (очевидно, для равных чисел в качестве «наибольшего» можно выбрать любое из них).
Возможен и алгоритм, использующий вложенные операторы ветвления (рис. 4.9).
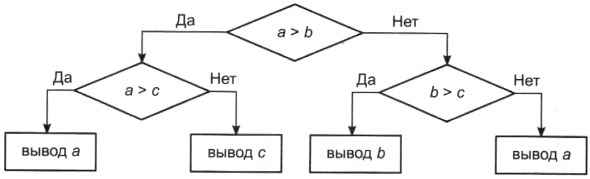
Рис. 4.9
Если требуется найти максимальное из четырёх и более чисел, то используется прием последовательного сравнения чисел с «предполагаемым максимумом». Сначала мы предполагаем, что максимальным является первое число. Далее каждое число по очереди сравнивается с текущим значением предполагаемого максимума: если это число больше, чем предполагаемый максимум, то в качестве предполагаемого максимума берётся уже это число. В результате после проверки всех чисел в переменной, в которой хранится предполагаемый максимум, окажется наибольшее число.
Мах = а
ЕСЛИ b>=Max ТО Мах = b
ЕСЛИ c>=Мах ТО Мах = с
ЕСЛИ d>=Max ТО Мах = d
Выполним трассировку алгоритма для исходных чисел 2, 3, 1, 5:
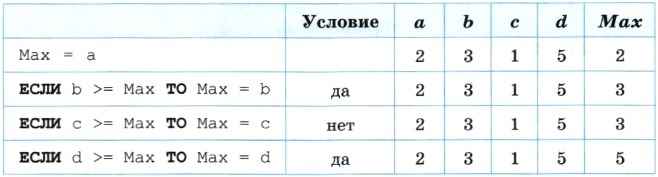
Алгоритм поиска наименьшего из двух, трёх, четырёх и более чисел реализуется аналогично, но в условиях операторов ветвления используется сравнение «меньше» (либо «меньше или равно»).
Подобный алгоритм обладает масштабируемостью: его легко дополнять для обработки практически любого количества чисел. Однако для поиска максимума или минимума из множества числовых значений удобнее использовать массивы и циклы.
Анализ записи числа в позиционной системе счисления (разбор числа на цифры)
Задано десятичное число. Требуется выделять и обрабатывать его отдельные цифры (от младших разрядов к старшим).
Принцип решения задачи
Для разбора числа на цифры используется пара операций, как правило, имеющихся в любом языке программирования:
• поиск остатка от деления (операция MOD);
• целочисленное деление (операция DIV).
Очевидно, что операция вычисления остатка от деления исходного числа на 10 приводит к выделению последней цифры этого числа. Например: 12345 MOD 10 = 5.
Операция целочисленного деления исходного числа на 10 приводит к «отсечению» последней цифры этого числа. Например: 12345 DIV 10 = 1234.
Соответственно, для разбора исходного числа X на отдельные цифры можно использовать цикл с предусловием:
Если использовать операции MOD и DIV для деления не на 10, а на другое число, то алгоритм будет выполнять разбор исходного числа на цифры соответствующей системы счисления. Например, использование операций MOD 2 и DIV 2 позволяет выделять цифры записи числа в двоичной системе счисления.
Поиск НОД заданных натуральных чисел
Заданы два натуральных числа. Требуется вычислить их наибольший общий делитель (НОД).
Принцип решения задачи
Операция поиска наибольшего общего делителя (НОД) двух заданных натуральных чисел обычно выполняется по алгоритму Евклида, который был впервые описан греческим математиком Евклидом около 300 лет до нашей эры. Идея алгоритма Евклида очень проста: из большего числа вычитается меньшее до тех пор, пока числа не станут равны. Полученное значение — это и есть НОД двух исходных чисел (рис. 4.10).
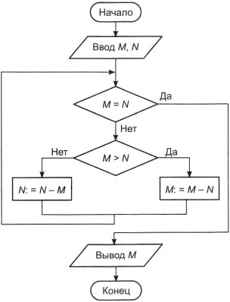
Рис. 4.10
Возможен также модифицированный алгоритм Евклида, работающий быстрее традиционного. Смысл модификации в том, что вместо последовательности нескольких одинаковых вычитаний меньшего числа из большего можно использовать операцию вычисления остатка от деления большего числа на меньшее. Например, для пары чисел 65 и 18:
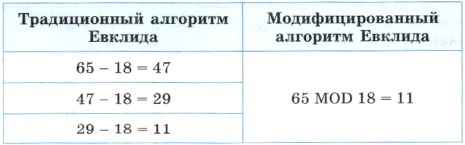
Для реализации модифицированного алгоритма Евклида используются две вспомогательные переменные. Кроме того, перед началом работы алгоритма необходимо обеспечить, чтобы первое из чисел обязательно было больше второго.
Выполним трассировку алгоритма для пары чисел 156 и 15:
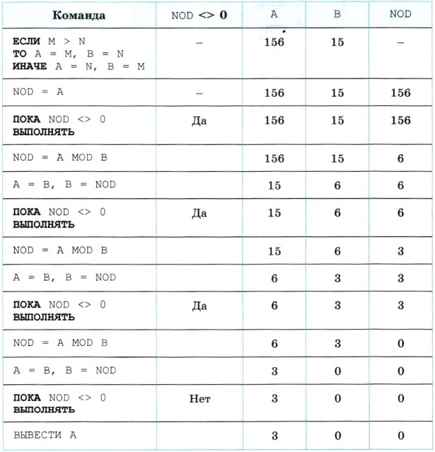
Вы можете самостоятельно оценить выгодность модифицированного алгоритма Евклида, заменив операции A MOD В на соответствующее количество операций вычитания числа В из числа А и определив их количество.
Проверка числа на простоту
Задано натуральное число. Требуется определить, является ли это число простым.
Простое число — это натуральное число, которое делится нацело только на единицу или на само себя.
Принцип решения задачи
Обычно такая задача решается методом перебора делителей — берётся исходное число N, и производятся попытки разделить его нацело на все натуральные числа от 2 до N - 1. При этом заранее предусматривается отдельная переменная-флаг:
• изначально ей присваивается значение, которое будет обозначать, что деление нацело невозможно (например, значение 0);
• в цикле имеется оператор ветвления, условие которого проверяет, делится ли исходное число нацело на очередной проверяемый делитель; если да, то в переменную-флаг записывается другое значение (например, 1).
После завершения работы цикла отдельный оператор ветвления проверяет значение переменной-флага: если в ней осталось значение 0, то можно сделать вывод, что исходное число простое (ни один проверяемый делитель не подошёл), а если её значение изменилось на 1, это означает, что исходное число не простое.
Ниже приведен фрагмент алгоритма определения простоты числа N. Для корректного решения задачи нужно также добавить перед этим фрагментом операторы ветвления, контролирующие возможную ошибкуввода отрицательного или нулевого числа, а также числа, равного 1 (которое, как известно из математики, хотя и удовлетворяет условию «делится только на 1 и на само себя», но простым числом не является).
Можно сделать этот алгоритм более оптимальным. Вспомним, что составное число можно представить как произведение меньшего сомножителя на больший, например:
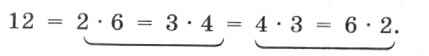
Обратите внимание на группы умножений, выделенные скобками: они «зеркально симметричны». А значит если деление исходного числа нацело обнаружено для какого-то из меньших сомножителей (в первой группе умножений они записаны первыми), то проверять соответствующие им большие сомножители уже не требуется. «Граница» между этими «симметричными» группами умножений примерно соответствует квадратному корню из исходного числа, поэтому в описанном выше алгоритме достаточно выполнять цикл не до N - 1, а до ближайшего натурального значения, большего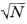 
. При этом используются две стандартные подпрограммы-функции, которые есть в любом языке программирования:
SQRT () — вычисление квадратного корня от значения, заданного в скобках;
INTO — определение целой части вещественного значения, заданного в скобках (в отличие от математической операции округления, эта функция просто отбрасывает дробную часть заданного числа, поэтому для округления в большую сторону нужно к полученному целому значению дополнительно прибавить единицу).
Вопросы и задания
1. Опишите основную идею алгоритмов поиска наибольшего/наименьшего из нескольких заданных чисел. Объясните принцип работы алгоритма поиска максимального/минимального значения путём последовательного сравнения чисел с предполагаемым максимумом/ минимумом.
2. Объясните принцип работы алгоритма разбора десятичной записи числа на отдельные цифры.
*3. Напишите на основе наразбора записи числа на отдельные цифры свой алгоритм перевода десятичного числа в его запись в двоичной системе счисления.
4. Объясните принцип работы модифицированного алгоритма Евклида. На примере определения НОД двух конкретных выбранных вами чисел продемонстрируйте и оцените выгодность модифицированного алгоритма Евклида по сравнению с традиционным (считайте для простоты, что каждая команда алгоритма выполняется в течение 0,1 секунды и сравните соответствующие затраты времени).
5. Как выполняется проверка заданного числа на простоту? Объясните суть идеи оптимизированного алгоритма проверки числа на простоту.
Cкачать материалы урока
