Урок 32
§2.4. Формула Шеннона
Содержание урока
Выбор правильной стратегии в игре «Угадай число»
Практическое задание «Определение количества информации»
Контрольные вопросы. Задания. Компьютерный практикум
Выбор правильной стратегии в игре «Угадай число»
На получении максимального количества информации строится выбор правильной стратегии в игре «Угадай число», в которой первый участник загадывает целое число (например, 3) из заданного интервала (например, от 1 до 16), а второй должен «угадать» задуманное число.
Если рассмотреть эту игру с информационной точки зрения, то начальная неопределенность знания для второго участника составляет 16 возможных событий (вариантов загаданных чисел).
При правильной стратегии интервал чисел всегда должен делиться пополам, тогда количество возможных событий (чисел) в каждом из полученных интервалов будет одинаково и их отгадывание равновероятно. В этом случае на каждом шаге ответ первого игрока («Да» или «Нет») будет нести максимальное количество информации (1 бит).
Как видно из табл. 2.1, угадывание числа 3 произошло за четыре шага, на каждом из которых неопределенность знания второго участника уменьшалась в два раза за счет получения сообщения от первого участника, содержащего 1 бит информации. Таким образом, количество информации, необходимой для отгадывания одного из 16 чисел, составило 4 бита.
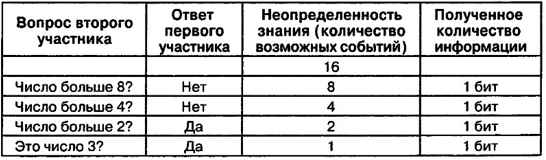
Таблица 2.1. Информационная модель игры «Угадай число»
Следующая страница 
Практическое задание «Определение количества информации»
Cкачать материалы урока
