Уроки 74 - 78
§3.3. Логические основы устройства компьютера

Содержание урока

3.3.1. Базовые логические элементы

3.3.2. Сумматор двоичных чисел

Полусумматор

Полный одноразрядный сумматор

Контрольные вопросы. Компьютерный практикум

3.3.3. Триггер

3.3.2. Сумматор двоичных чисел

Полный одноразрядный сумматор

Рассмотрим схему сложения двух n-разрядных двоичных чисел а_n ...а_iа_i-1...а₀ и b_n ...b_ib_i-1...b₀:

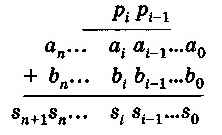
При сложении цифр i-го разряда складываются a_i и b_i, а также p_i-1 — перенос из i-1-го разряда. Результатом будет s_i — сумма и p_i — перенос в старший разряд. Одноразрядный двоичный сумматор — это устройство с тремя входами и двумя выходами.

Таким образом, полный одноразрядный сумматор должен иметь три входа: А, В — слагаемые и Р₀ — перенос из младшего разряда и два выхода: сумму S и перенос Р. Таблица сложения в этом случае будет иметь следующий вид (табл. 3.15).

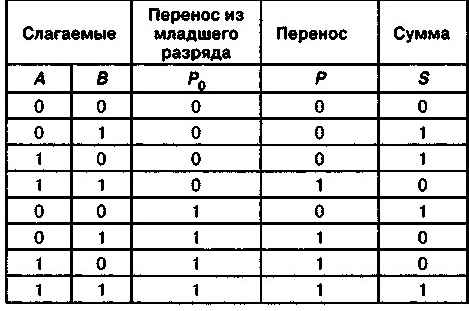
Таблица 3.15. Таблица сложения одноразрядных двоичных чисел с учетом переноса из младшего разряда

Идея построения полного сумматора точно такая же, как и полусумматора. Из таблицы сложения видно, что перенос (логическая переменная Р) принимает значение 1 тогда, когда хотя бы две входные логические переменные одновременно принимают значение 1. Таким образом, перенос реализуется путем логического сложения результатов попарного логического умножения входных переменных А, В, Р₀. Формула переноса получает следующий вид:

Р = (А & В) ∨ (А & P₀) ∨ (В & Р₀).

Для получения значения суммы (логическая переменная S) необходимо результат логического сложения входных переменных А, В, Р₀ умножить на инвертированный перенос P:

S=(A ∨ B ∨ P₀) & P.

Данное логическое выражение дает правильные значения суммы во всех случаях, кроме одного, когда все входные логические переменные принимают значение 1. Действительно:

Р = (1 & 1) ∨ (1 & 1) ∨ (1 & 1) = 1,

S = (1 ∨ 1 ∨ 1) & P = 1 & 0 = 0.

Для получения правильного значения суммы (для данного случая переменная S должна принимать значение 1) необходимо сложить полученное выше выражение для суммы с результатом логического умножения входных переменных А, В, Р₀. В результате логическое выражение для вычисления суммы в полном сумматоре принимает следующий вид:

S = (A ∨ В ∨ P₀) & P₀ ∨ (A & В & Р₀).

Теперь можно построить логическую схему полного одноразрядного сумматора (рис. 3.15).

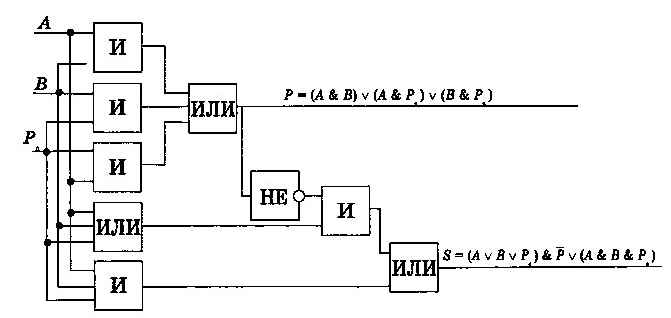
Рис. 3.15. Сумматор двоичных чисел

Многоразрядный сумматор процессора состоит из полных одноразрядных сумматоров. На каждый разряд ставится одноразрядный сумматор, причем выход (перенос) сумматора младшего разряда подключен ко входу сумматора старшего разряда.

Следующая страница Контрольные вопросы. Компьютерный практикум

Cкачать материалы урока