Уроки 58 - 60
Уточнение понятие алгоритма. Универсальные исполнители
§34. Уточнение понятия алгоритма

Содержание урока

Зачем нужно определение алгоритма?

Что такое алгоритм?

Универсальные исполнители

Машина Тьюринга

Машина Поста

Нормальные алгорифмы Маркова

Вопросы и задания

Задачи

Машина Поста

Практически одновременно с Тьюрингом (в том же 1936 г.) и независимо от него американский математик Э. Л. Пост предложил ещё более простую систему обработки данных, на основе которой позднее была построена так называемая машина Поста.

Лента в машине Поста (так же как и в машине Тьюринга) бесконечна и разбита на ячейки. Каждая ячейка может содержать метку (быть отмечена) или не содержать её (пустая ячейка) (рис. 5.6).

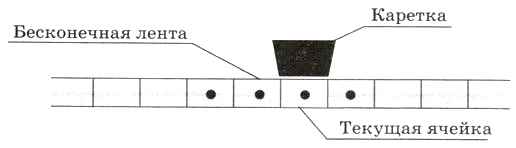
Рис. 5.6

Таким образом, Пост сократил алфавит всего до двух цифр. Это допустимо, потому что любые данные можно перекодировать в двоичный код, сопоставив каждой букве исходного алфавита уникальную последовательность нулей и единиц.

Кроме того, алгоритм работы машины Поста задаётся не в виде таблицы, а как программа, состоящая из отдельных команд. Система команд машины Поста содержит только 6 команд:

← — переместить каретку на 1 ячейку влево;
→ — переместить каретку на 1 ячейку вправо;
0 — стереть метку в рабочей ячейке (записать 0);
1 — поставить метку в рабочей ячейке (записать 1);
? n₀, n₁ — если в рабочей ячейке нет метки, перейти к строке n₀, иначе перейти к строке n₁;
стоп — остановить машину.

Попытка стереть метку там, где её нет, или поставить метку повторно считается ошибкой, и машина аварийно останавливается.

Все строки в программе нумеруются по порядку, это необходимо для работы команды ветвления (? n₀, n₁). С помощью этой команды можно также строить циклы как с предусловием, так и с постусловием. Например, следующая программа перемещает каретку влево до первой отмеченной ячейки:

1. ←
2. ? 1,3
3. стоп

Если после выполнения команды ←, →, 0 или 1 требуется перейти не на следующую строку, а на какую-то другую, то номер этой строки можно записать в конце команды. Например, команда

← 3

означает «переместить каретку влево и перейти на строку 3».

При работе с машиной Поста числа обычно записывают в унарной (единичной) системе счисления, в виде непрерывной цепочки меток нужной длины (вспомните счётные палочки в младшей школе). Например, на ленте, показанной на рис. 5.6, записано число 4.

Пост предположил, что любой алгоритм может быть записан как программа для предложенного им исполнителя. В теории алгоритмов доказано, что машины Поста и Тьюринга одинаковы по своим возможностям. Это значит, что круг задач, который они решают, тоже одинаков.

Следующая страница Нормальные алгорифмы Маркова

Cкачать материалы урока