Уроки 84 - 87
Динамическое программирование
(§45. Динамическое программирование)

Содержание урока

Что такое динамическое программирование?

Поиск оптимального решения

Количество решений

Вопросы и задания

Задачи

Что такое динамическое программирование?

Мы уже встречались с последовательностью чисел Фибоначчи (см. учебник для 10 класса):

F₁ = F₂ = 1; F_n = F_n-1 + F_n-2 при n > 2.

Для их вычисления можно использовать рекурсивную функцию:

function Fib(N: integer): integer;
begin
	if N<3 then
		Fib:=1
	else Fib:=Fib(N-l)+Fib(N-2);
end;

Каждое из этих чисел связано с предыдущими, вычисление Fa приводит к рекурсивным вызовам, которые показаны на рис. 6.35. Таким образом, мы два раза вычислили F₃, три раза — F₂ и два раза — F₁ Рекурсивное решение очень простое, но оно неоптимально по быстродействию: компьютер выполняет лишнюю работу, повторно вычисляя уже найденные ранее значения.

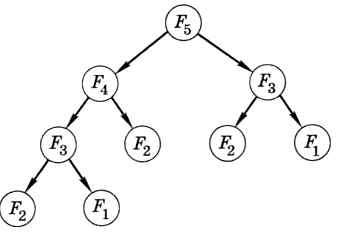
Рис. 6.35

Где же выход? Например, можно хранить все предыдущие числа Фибоначчи в массиве. Пусть этот массив называется F:

const N = 10;
var F: array[1..N] of integer;

Тогда для вычисления всех чисел Фибоначчи от Fx до FN можно использовать цикл:

F[1]:=1; F[2]:=1;
for i:=3 to N do
F[i]:=F[i-1]+F[i-2];

Динамическое программирование — это способ решения сложных задач путем сведения их к более простым подзадачам того же типа.

Такой подход впервые систематически применил американский математик Р. Беллман при решении сложных многошаговых задач оптимизации. Его идея состояла в том, что оптимальная последовательность шагов оптимальна на любом участке.

Например, пусть нужно перейти из пункта А в пункт Е через один из пунктов В, С или D (на рис. 6.36 числами обозначена «стоимость» маршрута).

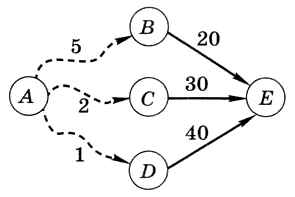
Рис. 6.36

Пусть уже известны оптимальные маршруты из пунктов В, С и D в пункт Е (они обозначены сплошными линиями) и их «стоимость». Тогда для нахождения оптимального маршрута из А в Е нужно выбрать вариант, который даст минимальную стоимость по сумме двух шагов. В данном случае это маршрут А-В-Е, стоимость которого равна 25. Как видим, такие задачи решаются «с конца», т. е. решение начинается от конечного пункта.

В информатике динамическое программирование часто сводится к тому, что мы храним в памяти решения всех задач меньшей размерности. За счёт этого удаётся ускорить выполнение программы. Например, на одном и том же компьютере вычисление F₄₅ с помощью рекурсивной функции требует около 8 секунд, а с использованием массива — менее 0,01 с.

Заметим, что в данной простейшей задаче можно обойтись вообще без массива:

f2:=1; f1:=1; 
for i:=3 to N do begin 
	FN:=f1+f2; 
	f2:=f1; 
	f1:=FN; 
end;

Задача 1. Найти количество K_N цепочек, состоящих из N нулей и единиц, в которых нет двух стоящих подряд единиц.

При больших N решение задачи методом перебора потребует огромного времени вычисления. Для того чтобы использовать метод динамического программирования, нужно:

1) выразить K_N через предыдущие значения последовательности K₁, K₂, ..., K_N-1;

2) выделить массив для хранения всех предыдущих значений К_i (i = 1, ..., N- 1).

Самое главное — вывести рекуррентную формулу, выражающую K_N через решения аналогичных задач меньшей размерности. Рассмотрим цепочку из N битов, первый элемент которой — О (рис. 6.37).

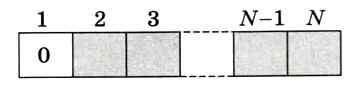
Рис. 6.37

Поскольку дополнительный O не может привести к появлению двух соседних единиц, подходящих последовательностей длины N с нулём в начале существует столько, сколько подходящих последовательностей длины N - 1, т. е. K_N-1 Если же первый символ — это 1, то вторым обязательно должен быть 0, а остальная цепочка из N - 2 битов должна быть правильной, без двух соседних единиц (рис. 6.38). Поэтому подходящих последовательностей длиной N с единицей в начале существует столько, сколько подходящих последовательностей длины N - 2, т. е. K_N-2.

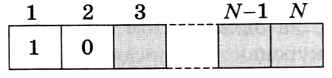
Рис. 6.38

В результате получаем: K_N = K_N-1 + K_N-2. Значит, для вычисления очередного числа нам нужно знать два предыдущих.

Теперь рассмотрим простые случаи. Очевидно, что есть две последовательности длины 1 (0 и 1), т. е. К₁ = 2. Далее, есть 3 подходящих последовательности длины 2 (00, 01 и 10), поэтому К₂ = 3. Легко понять, что решение нашей задачи — число Фибоначчи: K_N = F_n+2.

Следующая страница Поиск оптимального решения

Cкачать материалы урока